Che cos’è l’eccentricità dell’ellisse? Quali formule utilizzare per poterla calcolare? In questa lezione vedremo tutto ciò che c’è da sapere sull’eccentricità di un ellisse, dalla definizione agli esercizi svolti.
Definizione di eccentricità ellisse
L’eccentricità dell’ellisse è un parametro utile a capire quanto questa figura geometrica sia schiacciata sul suo asse maggiore. Matematicamente si calcola facendo il rapporto tra la distanza tra i due fuochi e la lunghezza dell’asse maggiore.
Nella lezione riepilogativa sull’ellisse, abbiamo detto che l’equazione canonica è: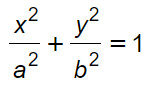
dove:
- a = semilunghezza dell’asse maggiore
- b = semilunghezza dell’asse minore
Abbiamo anche visto che se a>b abbiamo un ellisse con asse maggiore coincidente con l’asse delle y. Se b<a, coincide invece con l’asse delle x. Per ciascuno di questi due casi, l’eccentricità e si calcola con una formula differente.
Eccentricità ellisse ad asse maggiore orizzontale
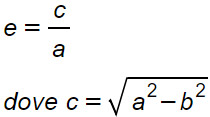
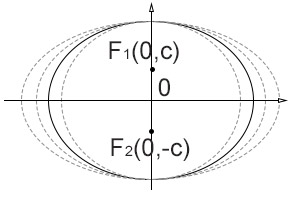
Maggiore è l’eccentricità dell’ellisse e più questa tenderà ad “allargarsi”, cioè a schiacciarsi sul suo asse principale. I casi limite sono due:
- e=1 → in questo caso l’eccentricità è massima, cioè c=a. L’ellisse si trasforma in una circonferenza.
- e=0 → l’eccentricità dell’ellisse è minima, per cui la figura si schiaccia così tanto da trasformarsi in un segmento.
Eccentricità ellisse ad asse verticale
In questo secondo e ultimo caso vale esattamente quanto detto nel caso precedente. L’unica cosa che cambia è la formula per calcolare l’eccentricità dell’ellisse. Questa volta al denominatore ci sarà il coefficiente b.
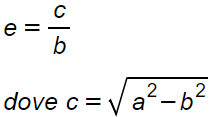
Esercizi sull’eccentricità dell’ellisse
Problema 1
Calcolare l’eccentricità dell’ellisse la cui equazione nel piano cartesiano è:
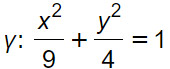
Svolgimento
Con i dati a disposizione possiamo dire che a²=9 e b²=4. Per cui possiamo calcolare subito a=3 e b=2. Per determinare l’eccentricità abbiamo bisogno anche del coefficiente c.
c = √(a²-b²) = √(9-4) = √5
Per cui l’eccentricità dell’ellisse vale:
e=c/a= √5/3
Problema 2
Calcolare l’eccentricità dell’ellisse la cui equazione nel piano cartesiano è:
![]()
Svolgimento
Attenzione a non lasciarti trarre in inganno dall’equazione dell’ellisse che ci viene fornita dalla traccia. Sappiamo che nell’equazione canonica ci sono dei denominatori sia alla x e che alla y. Per cui è necessario trasformare la seguente equazione in:
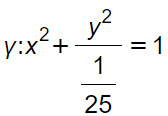
A questo punto possiamo calcolare i parametri a e b dell’ellisse. In particolare, poiché sotto la variabile x non c’è nulla, si assume che sia sottintenso 1. Per cui a=1. Sotto la variabile y c’è invece 1/25, per cui il parametro b=1/5. Possiamo così calcolare c con la solita formula:
c = √(a²-b²) = √(1-1/25) = √(24/25)
Abbiamo la radice di 24. Ti ricordi le regole delle radici? √24 = 2√6
c = 2√6/5
Possiamo infine calcolare l’eccentricità dell’ellisse:
e=c/a= 2√6/5
Conclusioni
Riepilogando quando visto in questa lezione: l’eccentricità è un parametro che misura lo schiacciamento dell’ellisse rispetto al suo asse maggiore. Ci sono due formule molto simili da seguire a seconda che i fuochi siano sull’asse x o sull’asse y. Gli esercizi sono molto semplici, l’importante è risolvere usando le formule viste passo passo.
Se questa lezione ti è stata utile o se hai dei dubbi o delle domande da porci, lascia un commento in basso. Ci aiuterai a migliorare la qualità di appunti ed esercizi che ogni giorno ti mettiamo a disposizione.