Come calcolare un binomio alla quarta? Esistono delle formule o un metodo di rapido calcolo? In questa guida vedremo come elevare alla quarta potenza un binomio generico. Analizzeremo nel dettaglio come svilupparlo nel caso in cui ci siano anche dei segni negativi.
Il binomio alla quarta non è altro che una potenza di grado 4 a cui bisogna elevare un generico binomio (a+b). Per ora non ci interessano i segni, vediamo innanzitutto come si fa il binomio alla quarta.
La regola di Tartaglia
In una precedente lezione abbiamo già parlato del triangolo di Tartaglia per lo sviluppo dei binomi di grado superiore al secondo. Se vai un attimo a rileggerti la lezione, troverai che avevamo ricavato questo piccolo schema numerico:

Come puoi vedere c’è un insieme di numeri in corrispondenza di ogni tipo di potenza. Accanto al binomio alla quarta (a+b)^4 troviamo i numeri:
1 4 6 4 1
Questi non sono altro che i coefficienti che andremo ad utilizzare per sviluppare il binomio alla quarta. Ciò significa che lo sviluppo di questa operazione algebrica porta alla formazione di 5 elementi che si sommano (o sottraggono). Vediamo quali sono.
Sviluppo binomio alla quarta
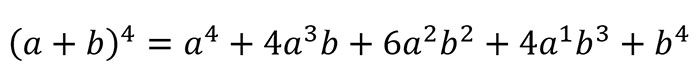
Come siamo arrivati a questa formula? Vediamo passo passo come fare.
Passo 1
Il binomio è composto da 2 monomi: +a e +b. La seconda osservazione da fare è che il grado massimo da raggiungere è 4 (perché è un binomio alla quarta), mentre si parte da un grado minimo zero.
Fatte queste due premesse, il primo termine del binomio elevato alla quarta è dato da:
il primo monomio elevato al grado massimo per il secondo monomio elevato al grado minimo.
Cioè:
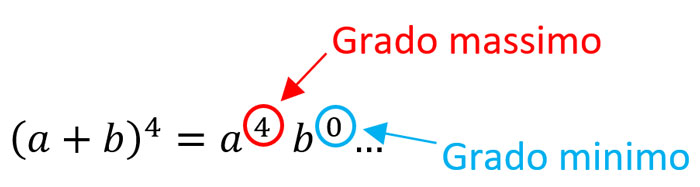
Nota: ci siamo disinteressati del coefficiente da mettere prima di a perché il primo termine è sempre 1.
Passo 2
A questo punto mettiamo un bel segno + e continuiamo con lo svolgimento. Inseriamo il secondo coefficiente di Tartaglia, abbassiamo di un grado l’esponente del primo monomio e alziamo quello del secondo monomio.
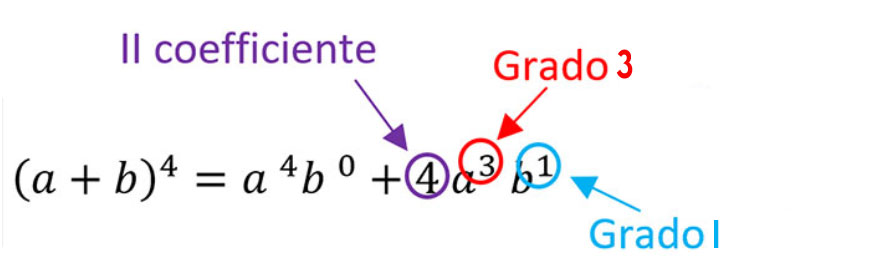
Passo 3
Ripetiamo la stessa identica operazione. Usiamo cioè il III coefficiente di Tartaglia, poi il primo monomio abbassato di 1 grado e il secondo aumentato di 1 grado.
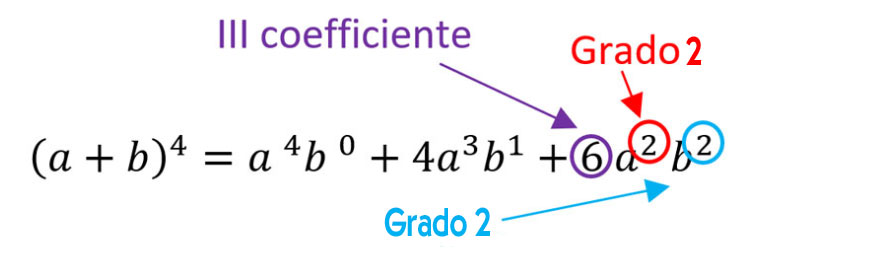
Passo 4
Prendiamo ora il quarto coefficiente, sulla a andrà il grado 1 mentre sulla b il grado 3.

Passo 5
Ultimo step: si prende l’ultimo coefficiente, il grado 0 della a e il grado 4 della b.

NOTA: hai visto come il primo termine della somma e l’ultimo abbiano una potenza alla 0? Ricordati che quel termine fa 1.
Binomio alla quarta (a-b)^4
Vediamo che cosa succede quando abbiamo il segno meno tra i due termini.
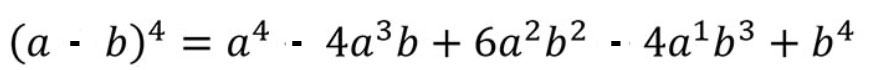
Una regola molto pratica è quella di alternare i segni. Parti dal primo positivo e poi uno si e uno no metti un segno meno.
Ciò è dovuto al fatto che il secondo e il quarto termine del polinomio hanno indice di potenza dispari, per cui conservano il segno meno.
Esercizi
Risolvere il binomio alla quarta (x+2)^4
Svolgimento
Applichiamo passo passo la regola vista in precedenza. Per cui, visto che i coefficienti restano sempre gli stessi (1 4 6 4 1) possiamo direttamente scrivere la soluzione.
Ricordati per ogni monomio che scrivi di diminuire di grado il primo ed aumentare il secondo.
(x-2)^4 = (x)^4(-2)^0 – 4(x)^3(-2)^1 + 6(x)^2(-2)^2 + 4(x)^1(-2)^3 + 1(x)^0(-2)^4
Eseguendo i calcoli e le semplificazioni diventa:
(x-2)^4 = x^4 – 8x^3 + 24x^2 -32x +16