Segmenti adiacenti e consecutivi – definizioni e immagini di esempio

Quelle di segmenti adiacenti e consecutivi sono due definizioni spesso difficili per gli studenti. In questa lezione vedremo che cosa sono i segmenti consecutivi e i segmenti adiacenti in geometria euclidea, dando una definizione precisa e vedendo delle immagini di esempio.

Innanzitutto che cos’è un segmento? Dalla definizione di retta sappiamo che quest’ultima è un insieme di punti allineati senza un’origine e una fine. Il segmento è semplicemente una parte di retta compresa tra due punti, detti estremi del segmento.

Per capire cosa sono i segmenti consecutivi e adiacenti introduciamo il semplice concetto di prolungamento. Prova a guardare l’immagine che segue come esempio.

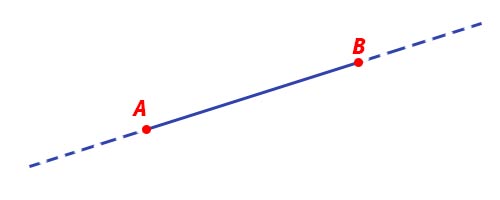
AB è il segmento in genere si dice anche che è la linea che congiunge A e B. Questa linea, che è la distanza più breve tra i due estremi, viene anche chiamata distanza tra due punti A e B.

Si può notare inoltre che prolungando A e B si ottengono delle semirette. La prima ha come origine A e prosegue in basso a sinistra nella figura, mentre la seconda parte da B e prosegue in alto a destra. Queste due semirette appartengono alla retta r che ha originato il segmento e si chiamano prolungamenti del segmento AB.

Segmenti consecutivi

Due segmenti sono consecutivi se hanno un solo estremo in comune.

La definizione di segmenti consecutivi non lascia spazio ad interpretazioni. Ci troviamo di fronte a due segmenti consecutivi quando hanno un estremo in comune. Ma attenzione: non è detto che siano allineati sulla stessa retta! Vediamo graficamente che cosa significa…

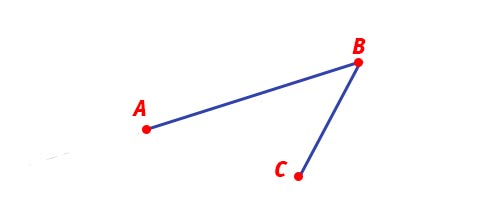
Nell’immagine puoi vedere 2 segmenti (AB e BC). Questi hanno 1 punto in comune ad una delle loro estremità. In particolare i segmenti AB e BC hanno l’estremo B in comune. Per questa ragione AB e BC sono segmenti consecutivi non allineati.

Proviamo a vedere un esempio più complesso composto da tanti segmenti.

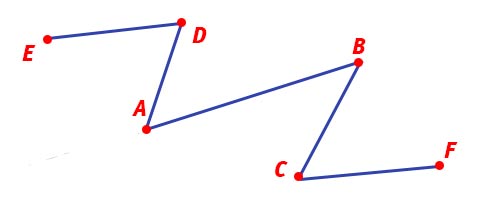
Come puoi vedere, in questo esempio abbiamo ben 5 segmenti: ED, AD, AB, BC e CF.

• ED e AD hanno l’estremo D in comune per cui sono consecutivi;
• AD e AB hanno l’estremo A in comune per cui sono consecutivi;
• BC e AB hanno l’estremo B in comune per cui sono consecutivi;
• BC e CD hanno l’estremo F in comune per cui sono consecutivi;

Una figura composta da tanti segmenti consecutivi tra loro viene detta spezzata. Una linea spezzata può essere aperta, come nel disegno che ti abbiamo mostrato, oppure chiusa. In quest’ultimo caso il punto E va a coincidere con F e si possono creare forme più note come ad esempio quelle dei poligoni. Pensa infatti ad un quadrato: questo non è altro che un insieme di 4 segmenti consecutivi e perpendicolari che formano un linea spezzata chiusa.

Per una maggiore chiarezza, ecco come sono fatti i segmenti consecutivi e perpendicolari:

Ma cosa succede quando ci troviamo di fronte a dei segmenti consecutivi che appartengono alla stessa retta, cioè sono allineati sulla stessa direzione? Ecco che dobbiamo dare la seconda definizione…

Segmenti adiacenti

Due segmenti sono adiacenti se sono consecutivi e se appartengono ad una stessa retta.

Quindi rispetto alla definizione precedente, è importante individuare la retta d’origine. In termini più semplici è sufficiente verificare che i due segmenti siano allineati. Vediamo dal punto di vista grafico cosa vuol dire…

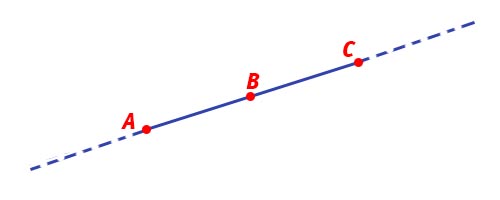Due segmenti adiacenti hanno lo stesso sostegno, cioè appartengono alla stessa retta r.

Segmenti adiacenti consecutivi o incidenti

A questo punto ti starai chiedendo qual è la differenza tra segmenti adiacenti e consecutivo con gli incidenti. Semplicemente in quest’ultimo caso i due segmenti hanno un punto in comune che non è un estremo. Quindi si ha una vera e propria intersezione tra i due segmenti. Invece nel caso di segmenti consecutivi ed adiacenti il punto in comune è uno dei due estremi.

Due segmenti adiacenti non consecutivi

Alcuni studenti ci hanno chiesto se due segmenti adiacenti possono non essere consecutivi. Per definizione due segmenti sono adiacenti quando hanno un punto in comune (quindi devono essere consecutivi) e sono allineati sulla stessa retta.

Questo implica che due segmenti consecutivi possono non essere adiacenti, ma due segmenti adiacenti non possono non essere consecutivi.