Trovare l’intersezione tra due rette significa calcolarne il punto in comune che hanno nel piano cartesiano. In questa pagina vedremo quali sono i metodi più usati e quelli consigliati per calcolare il punto di intersezione di due rette avendo a disposizione le coordinate cartesiane.
La premessa è che le rette non siano tra loro parallele. In questo caso, infatti, non esiste un punto di intersezione e andremmo a fare dei calcoli inutili. Ricordi come si fa a stabilire in geometria analitica se due rette sono parallele? Si va a verificare che non abbiano lo stesso coefficiente angolare.
Calcolo del punto di intersezione di due rette
Il metodo risolutivo che stiamo per analizzare può essere applicato all’intersezione di due rette, ma è valido per qualsiasi tipo di curva, che sia una circonferenza, una parabola, un’ellisse… la tecnica non cambia.
Per trovare il punto di intersezione tra rette, è sufficiente impostare un sistema di equazioni composto dalle equazioni della retta. Quindi al primo rigo metteremo l’equazione della prima retta, al secondo rigo ci sarà l’equazione della seconda retta.
Vediamo di spiegare con un esempio. Immaginiamo di dover trovare l’intersezione tra le due rette y=mr · x+qr e y=mr · x+qr, ti basta andare a risolvere un sistema in cui in ogni riga andrai a scrivere le due equazioni. Quindi metterai una parentesi graffa e poi le equazioni delle due rette una sopra l’altra (non ha importanza quale scrivi in alto e quale in basso). Ti sarà tutto più chiaro vedendo gli esercizi che ti riportiamo di seguito, assieme al risolutore online…
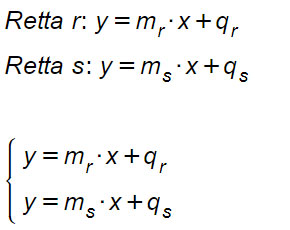
A questo punto la lezione vera e propria di geometria analitica è conclusa perché si passa ad un esercizio di algebra, cioè ad un sistema di primo grado da risolvere con uno dei metodi visti a lezione:
- sostituzione (il più usato dagli studenti)
- somma o differenza (il più rapido ma non sempre applicabile)
- confronto e Cramer (meno utilizzati)
Vediamo dei casi pratici, così da vedere praticamente come si calcola il punto di intersezione.
Esercizi sull’intersezione tra due rette
Esercizio 1
Determinare le coordinate del punto di intersezione tra le due rette r:y=1/4x-1/2 e s:y=-x+5
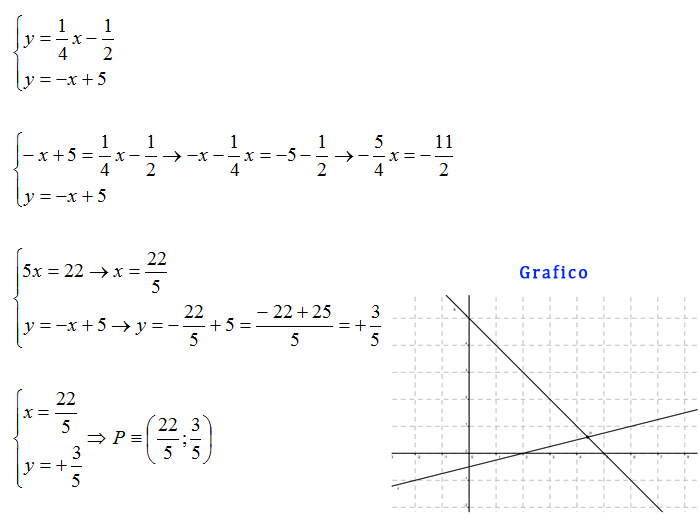
Come puoi vedere per risolvere il sistema è stato usato il metodo della sostituzione. Siamo arrivati rapidamente a trovare la soluzione dell’esercizio, calcolando le coordinate x ed y del punto di intersezione. Infine ti abbiamo incluso il grafico, che va sempre disegnato negli esercizi di geometria analitica.
Esercizio 2
Tracciare il grafico delle due rette e il loro punto di intersezione. r:y=-1/3x+2/3, s:y=3x-1/2
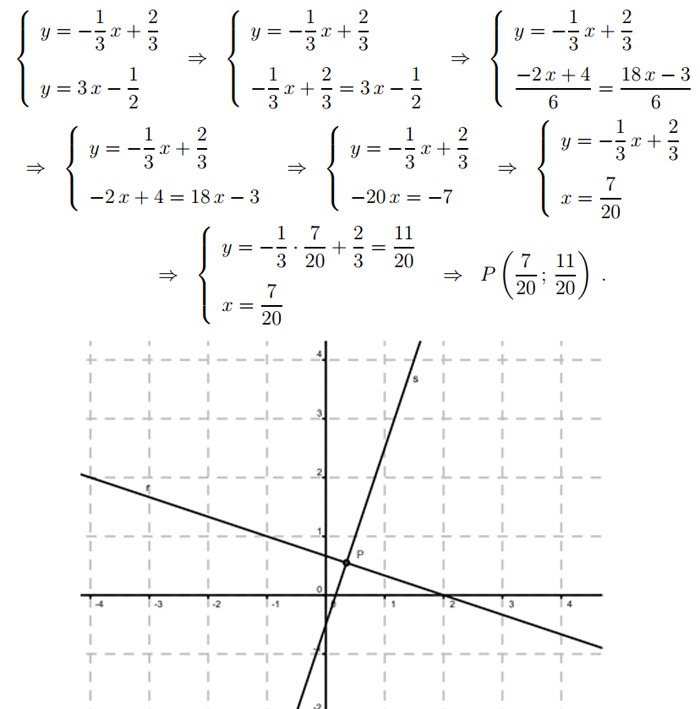
Esercizio 3
Determinare l’intersezione tra le due rette nel piano cartesiano. r: -4x+4y-12=0 e s:2x-y+5=0
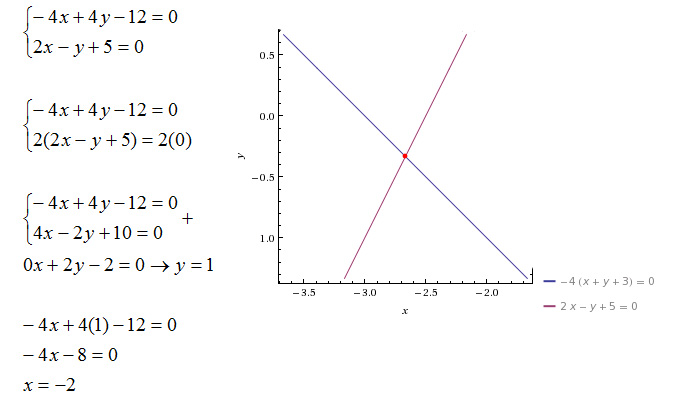
In questo caso l’esercizio, o meglio il sistema algebrico tra le due equazioni, è stato risolto usando il metodo della somma. E’ stato cioè moltiplicata la seconda equazione per 2 (entrambi i membri) così da ottenere lo stesso coefficiente della x (ma in segno opposto). A questo punto è bastato sommare le due equazioni per arrivare rapidamente alla soluzione.
Intersezione tra rette parallele e perpendicolari
Ti ricordi quali caratteristiche hanno in geometria analitica le rette parallele e perpendicolari nel piano cartesiano? Dicemmo che nel primo caso le rette hanno stesso coefficiente angolare (Esempio: m1=m2=3), nel secondo caso l’inverso e con il segno cambiato (Esempio: m1=2, m2=-1/2).
Dal punto di vista teorico, la spiegazione è molto semplice: le rette perpendicolari si risolvono come tutte le altre, non hanno nessuna differenza. Mentre le rette parallele non si intersecano mai, per cui ci troveremo di fronte ad un sistema impossibile. Non ci credi? Guarda questo esempio…
Cerca di trovare il punto di intersezione tra due rette parallele: y=x+1 e y=x+4.
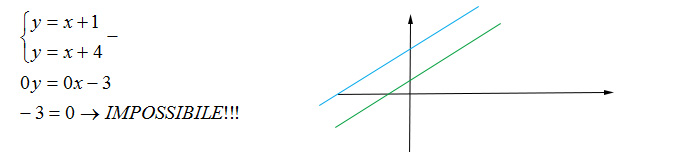
In questo facile esempio abbiamo usato il metodo della sottrazione per risolvere il sistema che, di fatto, è impossibile! Cioè non esistono punti di intersezione tra le due rette.
Se vuoi continuare ad esercitarti ti consigliamo questa piccola raccolta di esercizi sulle intersezioni tra rette del liceo Enrico Fermi di Roma -> scarica il file
Per dubbi, domande, suggerimenti o anche solo per una mano a risolvere i tuoi esercizi a casa, CONTATTACI, il nostro staff è a tua disposizione per aiutarti!