Una volta calcolati il seno e il coseno possiamo dare una definizione di tangente e cotangente di un angolo. In questa lezione troverai non solo la parte teorica ma anche una tabella con i valori di tangente e cotangente negli angoli più ricorrenti e alcuni esercizi svolti e commentati.
Definizione di tangente di un angolo
Tangente di 90 gradi
Definizione di cotangente di un angolo
Cotangente di 90 gradi
Valori tangente e cotangente di angoli noti
Esercizi svolti e con soluzione
Definizione di tangente di un angolo
Definizione di tangente: dato un triangolo rettangolo, la tangente è una funzione che si usa in goniometria definita come il rapporto tra il seno e il coseno dell’angolo:

Guardiamo la circonferenza goniometrica e capiamo cosa vuol dire. Dal punto di vista geometrico la tangente dell’angolo a è il segmento AT riportato sul grafico.
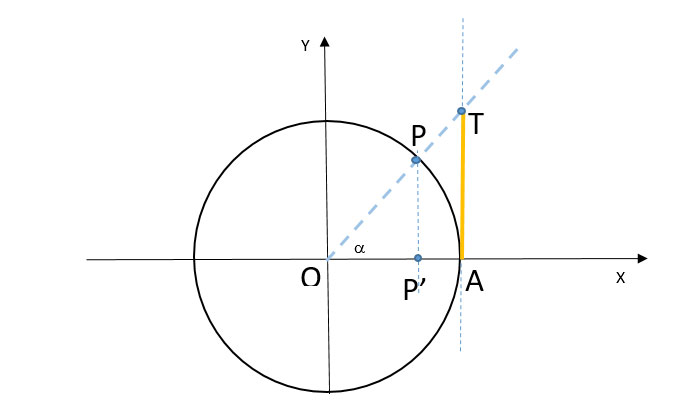
Grafico della tangente di un angolo
Notiamo che abbiamo due triangoli rettangoli: OPP’ e il triangolo rettangolo OAT. Essendo due angoli simili possiamo scrivere una proporzione tra i cateti:
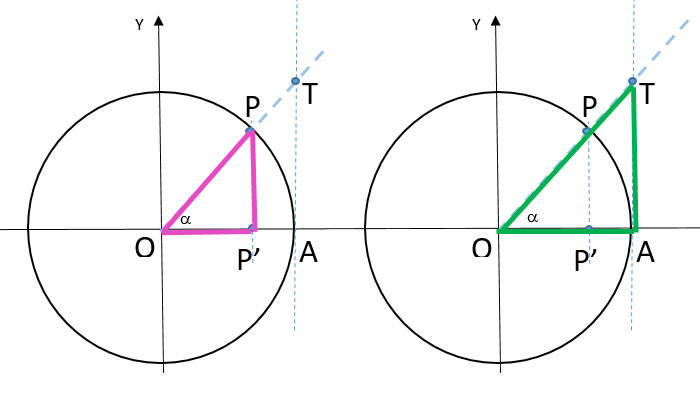
Tangente di un angolo definizione e costruzione
OP’: OA = P’P : AT
Dove ricaviamo AT che è proprio la tangente che stiamo cercando. Ricordando la definizione di seno e coseno possiamo ottenere che:

dove: P’P = sena, OP’= cosa, OA = 1 perché raggio della circonferenza goniometrica. Quindi sostituendo:

Ma inizialmente abbiamo notato che AT è la tangente dell’angolo a, quindi AT= tga. Ottenendo così la definizione di tangente:

Formula di tangente in funzione di seno e coseno
Tangente di un angolo di 90 gradi
Vi hanno detto in classe o avete letto sul vostro libro che “La tangente di 90° non esiste”, ma piuttosto che imparalo a memoria capiamo cosa vuol dire: guardate il disegno della circonferenza goniometrica in cui abbiamo scelto due angoli a e a’.
a è molto piccolo (si avvicina a zero)
a’ è molto grande (si avvicina a 90°)
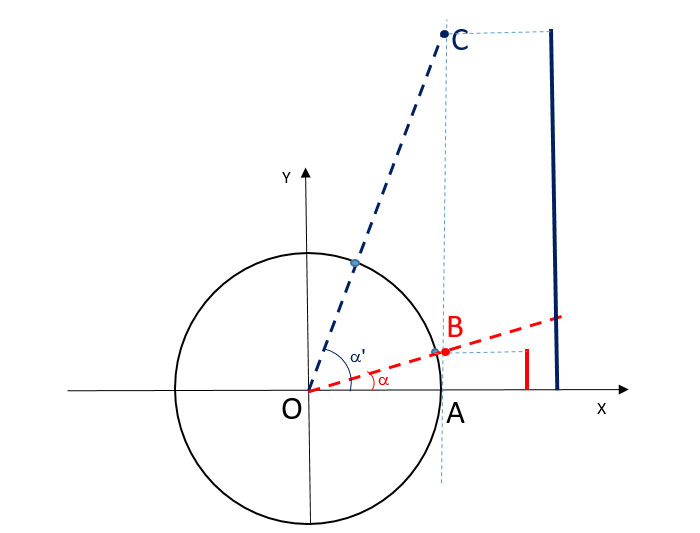
Se chiamiamo le relative tangenti AB e AC notiamo che AB è molto piccola, AC è molto grande. Per il calcolo della tangente possiamo così dire che:
- Quanto più a si avvicina allo 0 tanto più il segmento AB diventa piccolo, fino ad annullarsi.
- Quanto più a’ si avvicina ai 90° tanto più il segmento AC diventa grande, fino a che le due rette diventano parallele e non si incontrano mai!
Ecco perché diciamo che è impossibile calcolare la tangente a 90°, non può esistere o meglio non esiste la tangente di

Con k si indicano numeri reali interi, cioè 0, 1, 2, 3, 4…
In questo modo racchiudiamo in una sola formula tutti gli angoli pari: a = 90°+0, a = 90° + 180°, a = 90° + 360°…
Se hai qualche dubbio sull’unita di misura degli angoli puoi dare uno sguardo alla lezione sulla misura gli angoli in radianti e gradi.
Cos’è la cotangente di un angolo?
Definizione di cotangente: la cotangente di un angolo è definita come il rapporto tra il coseno ed il seno dello stesso angolo, o come il reciproco della sua tangente: Possiamo disegnare il grafico della cotangente dell’angolo a con il segmento GF.
Possiamo disegnare il grafico della cotangente dell’angolo a con il segmento GF.
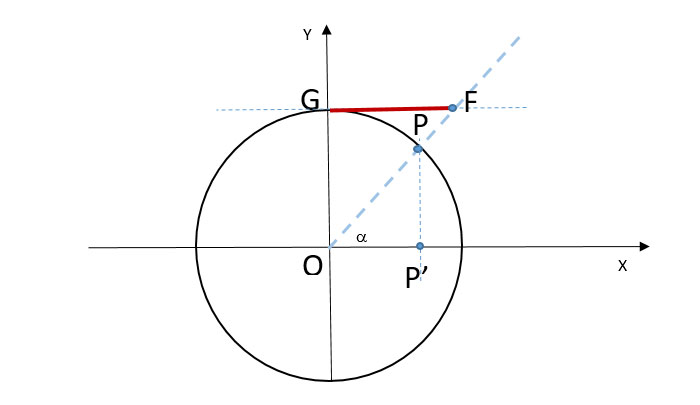
Considerando che i due triangoli rettangoli OGF e OPP’ sono simili, possiamo scrivere la proporzione:
GF : OP’ = OG : PP’
E ricordando la definizione di seno e coseno possiamo ottenere che OP’= cosa, P’P = sena e OG = 1 perché coincide con il raggio della circonferenza goniometrica.

E quindi la cotangente è il reciproco della tangente come dalla definizione:

Relazione tra tangente e cotangente
Cotangente di un angolo di 90 gradi
Come fatto per la tangente, per capire il valore della cotangente a 90°, guardiamo il disegno: abbiamo ancora due angoli a e a’.
a è molto piccolo (si avvicina a zero)
a’ è molto grande (si avvicina a 90°)
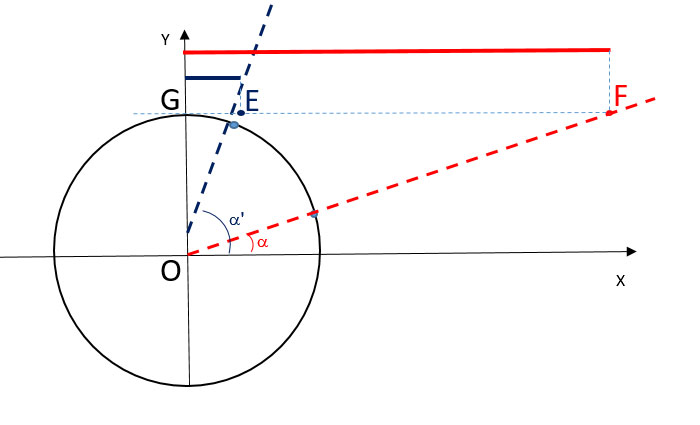
Se chiamiamo le relative cotangenti GF e GE notiamo che:
GF è molto grande
GE è molto piccola
- Quanto più a si avvicina allo 0 tanto più il segmento GF diventa grande, fino ad essere una retta parallela all’asse delle x;
- Quanto più a’ si avvicina ai 90° tanto più il segmento GE diventa piccolo, fino a diventare nullo.
Praticamente accade il contrario di quello che abbiamo visto per la tangente e quindi possiamo dire che la cotangente non esiste se:

E cioè diciamo che non è definita (assume valore infinito) la cotangente negli angoli pari: a = 0°, 180°, 360°…
Valori tangente e cotangente – Tabella con gli angoli noti
Ecco una tabella con i valori delle funzioni goniometriche tangente e cotangente in alcuni angoli notevoli.

Valori tangente e cotangente
Con i valori riportati in tabella e le formule di sottrazione e addizione, di duplicazione, di bisezione, e quelle parametriche è possibile calcolare il valore delle funzioni anche oltre i 90º combinandole in vari modi.
Esercizi svolti su tangente e cotangente
Ecco alcuni esercizi svolti utilizzando la tabella dei valori di tangente e cotangente:
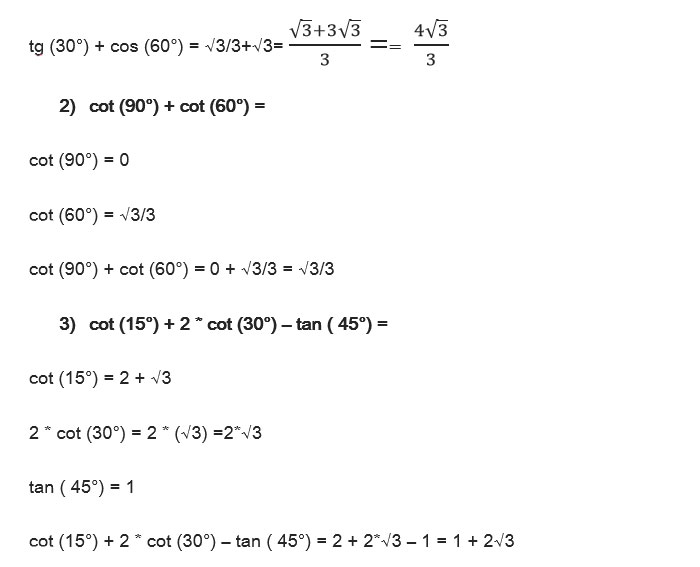
Ora puoi mettere alla prova le tua conoscenze con gli esercizi con soluzioni su tangente e cotangente:

Per le soluzioni degli esercizi, dubbi o problemi il nostro staff è a vostra disposizione per chiarimenti o lezioni private: contattaci.