Le operazioni con i monomi sono le operazioni algebriche di somma, differenza, prodotto e divisione tra monomi. Si tratta di calcoli che riguardano la parte numerica e letterale e che verranno poi utilizzati anche con i polinomi.
Proprio per questa ragione è importante imparare a risolvere le operazioni con i monomi in maniera rapida e senza avere difficoltà o dubbi. Se ti è già chiara la definizione di monomio, ecco elencate subito le operazioni principali che andremo a studiare in questa lezione.
Le 4 operazioni con i monomi
Somma Algebrica
Per comprendere pienamente le operazioni con i monomi è necessario che tu abbia capito perfettamente cosa sono i monomi simili e le operazioni con i numeri relativi. Se hai ben chiari questi due concetti, la somma algebrica sarà per te estremamente chiara.
Due o più monomi si possono sommare solo se sono simili; altrimenti ci limiteremo a scriverli uno di seguito all’altro con il proprio segno. Che significa? Vediamo un esempio di somma algebrica e tutti ci sarà più chiaro…
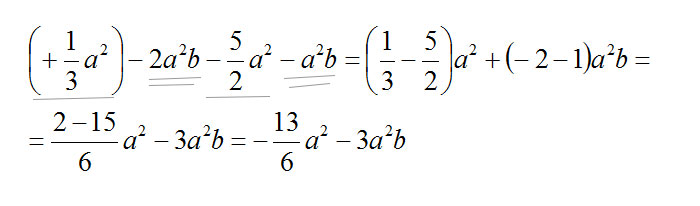
Per semplificarti la vita, mentre svolgi una somma algebrica ti consigliamo di sottolineare i termini simili in maniera differente tra loro. La differenza tra somma aritmetica e somma algebrica di monomi è evidente: nel primo caso hai solo dei numeri con le quattro operazioni fondamentali che si insegnano già alle scuole elementari. Con la somma algebrica di monomi devi tenere in considerazione del segno e della parte letterale.
Moltiplicazione tra monomi
La moltiplicazione tra monomi si esegue facendo il prodotto dei segni, il prodotto dei coefficienti e il prodotto delle lettere (per quest’ultima operazione ricordati le regole delle potenze e in particolare la moltiplicazione tra potenze con la stessa base). Ecco un esempio facile facile:
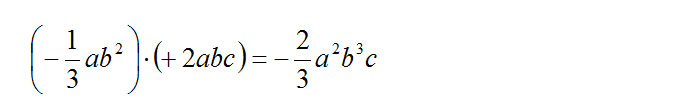
Divisione tra monomi
E’ tra le operazioni con i monomi più sbagliate dagli studenti durante i compiti, anche se la regola è perfettamente identica alla moltiplicazione.
Per fare la divisione tra monomi basta come sempre dividere i segni (il che equivale a moltiplicarli), dividere la parte numerica e dividere la parte letterale (per quest’ultima applicherai la divisione tra potenze con la stessa base).
Ciò che più è difficile per gli studenti non è tanto la parte letterale quanto la divisione tra frazioni! Ti ricordiamo che la divisione di frazione può essere eseguita trasformando il “diviso” in “per” e invertendo numeratore e denominatore del divisore (il secondo numero della divisione!). Vediamo subito un esempio:
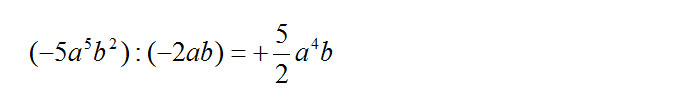
Come puoi vedere dall’esempio, se i monomi non sono divisibili, il loro quoziente sarà una frazione. Ciò ovviamente riguarda anche le lettere. Se al divisore infatti avessimo avuto (-2abc) allora nel risultato finale avremmo dovuto mettere la lettera c al denominatore.
Potenze
Per elevare a potenza un monomio si elevano a potenza il suo coefficiente numerico e la sua parte letterale. Ricordati: se la potenza ha indice dispari il segno si conserva, sia positivo che negativo. Se l’indice di potenza è pari il segno è sempre più! Vediamo un esempio:

Potenza di un monimio
Ricapitolando: nella somma algebrica di monomi, quindi addizione e sottrazione, è importante che i monomi siano simili. In tutti gli altri casi le operazioni con i monomi sono sempre eseguibili.
Se ti è tutto chiaro, puoi passare alla parte pratica: vai alla lezione dedicata agli esercizi sui monomi per trovare esempi ed esercizi svolti.
Nel caso in cui tu abbia ancora dubbi o perplessità, ti invitiamo a contattarci: risolveremo in brevissimo qualsiasi tuo dubbio.