Sistemi di equazioni goniometriche

In questa lezione vedremo come si risolvono i sistemi di equazioni goniometriche a due o più incognite. Vedremo quasi immediatamente degli esempi facili e proveremo ad analizzare i metodi usati per gli esercizi svolti sui sistemi goniometrici.

Nelle precedenti lezioni hai avuto modo di studiare le equazioni goniometriche, vedendo tutte le casistiche disponibili per affrontare e risolvere questa tipologia di esercizio, che spesso dà molte difficoltà agli studenti. Ovviamente per imparare a risolvere i sistemi è fondamentale che tu abbia capito bene non solo le equazioni goniometriche, ma anche i metodi per risolvere i sistemi.

Come si risolvono i sistemi di equazioni goniometriche?

Esempi ed esercizi svolti

Esercizi da svolgere

Come risolvere i sistemi di equazioni goniometriche

Per procedere con la risoluzione di un sistema goniometrico a due equazioni, cioè per trovare le soluzioni comuni alle due equazioni, a volte si può usare il metodo di sostituzione. Cioè si risolve una delle equazioni rispetto ad un’incognita e si sostituisce l’espressione trovata nell’altra equazione. A volte, però, capita che questo metodo non sia sufficiente e, soprattutto negli esercizi più difficili, occorre applicare degli artifizi – delle semplificazioni o sostituzioni – che permettano di semplificare l’esercizio da svolgere.

Esercizio svolto con il metodo di sostituzione

Questo primo esercizio è piuttosto semplice, ma prova a seguirlo ugualmente. E’ importante perché ti fa capire come si risolvono i sistemi di equazioni goniometriche con il metodo della sostituzione. Vediamo subito questo esempio allora… Risolviamo il seguente sistema.

sistemi-di-equazioni-goniometriche

Sostituiamo nella seconda equazione il valore di y ottenuto dalla prima ed applichiamo subito le regole viste con gli archi associati. Otteniamo quindi:

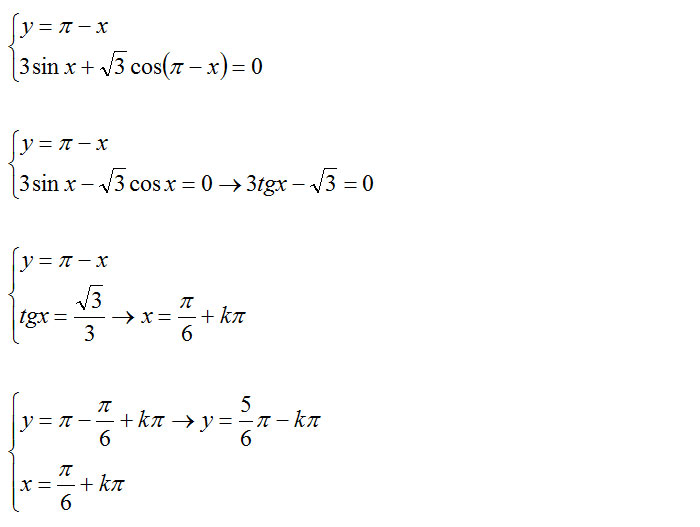
Risolvere il sistema con metodi alternativi

Proviamo a risolvere questo esercizio. Ad uno primo sguardo potrebbe sembrare semplice ma, se volessimo risolverlo con la sostituzione, dovremmo far ricorso alle formule di addizione e sottrazione e probabilmente anche alle formule di triplicazione. Vediamo allora un metodo più semplice per risolverlo:

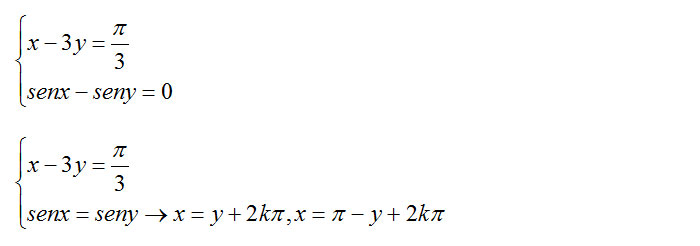
Poiché senx=seny, vuol dire che x=y oppure per le proprietà degli archi associati x=180-y. Abbiamo così individuato due valori di x, non ci resta che sostituire la prima equazione del sistema in quella così ottenuta per ottenere le due soluzioni.

Abbiamo quindi suddiviso il problema in due momenti diversi. Trovate le due soluzioni x che risolvono il sistema le abbiamo inserite (una alla volta) ottenendo così le due soluzioni finali. La parte più difficile è senza dubbio quella iniziale, dato che difficilmente lo studente si ferma a ragionare su come risolvere un sistema di equazioni.

Esercizio svolto con prostaferesi

Da un libro di testo abbiamo trovato un interessante esercizio che vogliamo mostrarti. Questa volta sono state usate le formule di prostaferesi per risolverlo. Ecco la traccia e la soluzione con tutti i passaggi. (trovi in seguito il commento e la spiegazione dell’esercizio)

Sono state qui utilizzate le Formule di Prostaferesi perché queste contengono al loro interno la somma degli argomenti delle funzioni trigonometriche seno e coseno. In questo modo è stato sufficiente applicare la prima equazione alla seconda trasformata per poter automaticamente eliminare il seno dal problema. Si è così trovata la soluzione del coseno considerando le due incognite (abbiamo cioè trovato x-y=…..). Si sostituisce di nuovo nella prima equazione del sistema goniometrico e si arriva rapidamente alla soluzione.