Nella lezione di oggi proveremo a risolvere assieme alcuni esercizi sui sistemi di primo grado: analizzeremo i vari metodi, dandone una nostra interpretazione, con consigli e suggerimenti per gli studenti.
Gli argomenti della lezione
Nella scorsa lezione abbiamo imparato come risolvere i sistemi di equazioni di primo grado. Abbiamo analizzato i vari metodi di risoluzione, soffermandoci su quelli in genere considerati più difficili dagli studenti. Oggi faremo esercizi di matematica sui sistemi di primo grado, ecco la traccia, buon lavoro.
Risolvere i seguenti sistemi di primo grado
Primo esercizio sui sistemi di primo grado
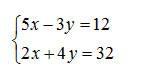
In questo primo esercizio sui sistemi di primo grado, non essendoci frazioni, consigliamo di optare per la strada più sbrigativa, cioè il metodo della somma e della differenza.
Iniziamo quindi a calcolare il minimo comune multiplo tra 5 e 2, cioè tutte le incognite della x. Potremmo allo stesso modo calcolare il mcm anche tra 3 e 4, cioè le incognite della y, non cambierebbe nulla nei calcoli e nel risultato. Tra 5 e 2 il mcm è pari a 10, per cui calcolo 10:5=2 (moltiplico per 2 tutta la prima equazione) e 10:2=5 (moltiplico per 5 tutta la seconda equazione del sistema di primo grado). Ottengo così: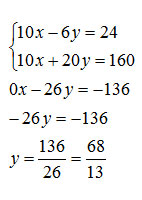
Poiché i coefficienti della x sono concordi, ho sottratto membro a membro le equazioni del sistema di primo grado, giungendo in questo modo a calcolare rapidamente la y.
A questo punto non mi resta che sostituirla in una delle equazioni della traccia per poter così calcolare l’altra incognita, cioè la x.
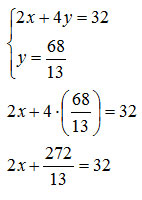
Ricordandoci come si risolvono le equazioni di primo grado, possiamo calcolare l’incognita x portando tutti i termini noti a destra.
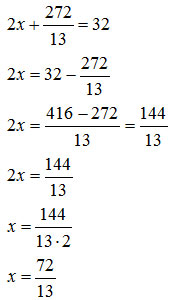
Avendo calcolato entrambe le incognite, l’esercizio è concluso.
Secondo esercizio sui sistemi di primo grado
Come è possibile vedere, nella traccia dell’esercizio ci sono dei denominatori numerici. Per eliminarli, come sempre, è necessario calcolare il minimo comune multiplo. Solo successivamente sarà possibile eliminarli:
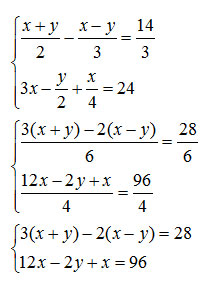
Pochi semplici passaggi sono stati sufficienti per ricondurmi al caso precedente, cioè ad un sistema di primo grado privo di frazioni. Bastano poche operazioni tra numeri relativi e incognite per semplificare il tutto eliminando le parentesi tonde:
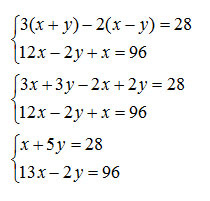
Questa volta, per cambiare, sfrutteremo il metodo di Cramer. Ricordiamo che il metodo di Cramer per i sistemi di primo grado, consiste nel calcolare i tre determinanti e poi dividerli tra loro, come già visto nelle lezione sui metodi per risolvere le equazioni di primo grado.
Attenzione a mettere bene in colonna i termini, cioè ad ordinare allo stesso modo le equazioni: prime le x, poi le y e al secondo membro da soli i termini noti. Ecco quindi le piccole matrici numeriche:
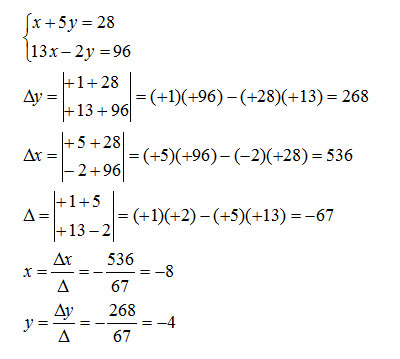
Abbiamo visto che il metodo di Cramer per i sistemi, così come il metodo di addizione e sostituzione è piuttosto rapido e, con un po’ di concentrazione porta a completare l’esercizio in maniera rapida.
Lasciamo a voi, come esercizio, provare che con il metodo della sostituzione il risultato sarebbe stato lo stesso, ma forse un po’ più complesso dal punto di vista dei calcoli.
Terzo esercizio sui sistemi di primo grado
Vogliamo ulteriormente complicare i calcoli, per cui decidiamo di proporvi di risolvere assieme un esercizio sui sistemi di primo grado con coefficienti letterali. Ricordandoci le operazioni base del calcolo letterale, proviamo a svolgere assieme questo breve esercizio con le lettere:
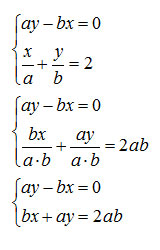
Ricordando che il minimo comune multiplo tra due semplici lettere si ottiene calcolando il prodotto delle due lettere, nel nostro caso mcm=ab, ci siamo ricondotti al caso più semplice.
Attenzione, però, che il sistema di primo grado non è correttamente ordinato. I coefficienti infatti fanno disposti nello stesso ordine, prima la x, poi la y e il termino noto al secondo membro. Fatto ciò mi rendo conto che l’esercizio può essere facilmente risolto con il metodo dell’addizione, per cui:
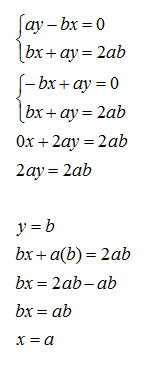
Compiti ed esercizi da svolgere
A questo punto vi invitiamo a risolvere la seguente pagina di esercizi sui sistemi di primo grado da soli. Per dubbi o curiosità restiamo ovviamente a vostra disposizione, non dovrete far altro che contattarci. Buon lavoro:

Nella prossima lezione introdurremo finalmente il concetto di disequazione. Vedremo infatti come risolvere le disequazioni di primo grado, con esercizi svolti e tanti esempi.