In questa pagina troverai la traccia della seconda prova di matematica 2016 per liceo scientifico completa di svolgimento e commenti da parte dei nostri docenti. Allenati a risolvere con noi la prova d’esame data nella maturità e preparati a sostenere l’esame di stato con maggiore serenità.
INDICE:
La traccia della seconda prova di matematica 2016
Tema di: MATEMATICA
Indirizzo: LICEO SCIENTIFICO
Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario
PROBLEMA 1
L’amministratore di un piccolo condominio deve installare un nuovo serbatoio per il gasolio da riscaldamento. Non essendo soddisfatto dei modelli esistenti in commercio, ti incarica di progettarne uno che risponda alle esigenze del condominio.
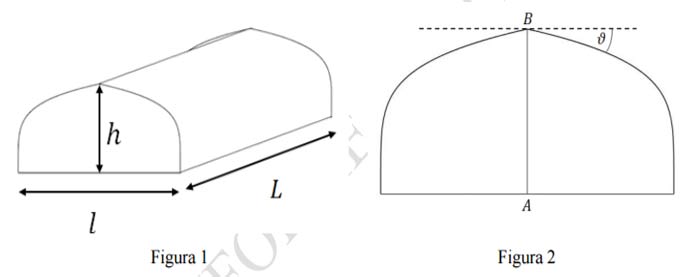
Allo scopo di darti le necessarie informazioni, l’amministratore ti fornisce il disegno in figura 1, aggiungendo le seguenti indicazioni:
- la lunghezza ? del serbatoio deve essere pari a 8 metri;
- la larghezza ? del serbatoio deve essere pari a 2 metri;
- l’altezza ℎ del serbatoio deve essere pari a 1 metro;
- il profilo laterale (figura 2) deve avere un punto angoloso alla sommità, per evitare l’accumulo di ghiaccio durante i mesi invernali, con un angolo ? ≥ 10°;
- la capacità del serbatoio deve essere pari ad almeno 13 m3 , in modo da garantire al condominio il riscaldamento per tutto l’inverno effettuando solo due rifornimenti di gasolio;
- al centro della parete laterale del serbatoio, lungo l’asse di simmetria (segmento ?? in figura 2) deve essere installato un indicatore graduato che riporti la percentuale di riempimento V del volume del serbatoio in corrispondenza del livello z raggiunto in altezza dal gasolio.
- Considerando come origine degli assi cartesiani il punto ? in figura 2, individua tra le seguenti famiglie di funzioni quella che meglio può descrivere il profilo laterale del serbatoio per ? ∈ [−1, 1], ? intero positivo, motivando opportunamente la tua scelta:
?1(?) = (1 − |?|)1/?
?2(?) = −6|?|3 + 9??2 − 4|?| + 1
?3(?) = ???(?/2 ?? ) - Determina il valore di ? che consente di soddisfare i requisiti richiesti relativamente all’angolo ? e al volume del serbatoio.
- Al fine di realizzare l’indicatore graduato, determina l’espressione della funzione ?(?) che associa al livello ? del gasolio (in metri) la percentuale di riempimento V del volume da riportare sull’indicatore stesso. Quando consegni il tuo progetto, l’amministratore obietta che essendo il serbatoio alto un metro, il valore ? del livello di gasolio, espresso in centimetri, deve corrispondere alla percentuale di riempimento: cioè, ad esempio, se il gasolio raggiunge un livello ? pari a 50 cm vuol dire che il serbatoio è pieno al 50%; invece il tuo indicatore riporta, in corrispondenza del livello 50 cm, una percentuale di riempimento 59,7%.
- Illustra gli argomenti che puoi usare per spiegare all’amministratore che il suo ragionamento è sbagliato; mostra anche qual è, in termini assoluti, il massimo errore che si commette usando il livello ? come indicatore della percentuale di riempimento, come da lui suggerito, e qual è il valore di ? in corrispondenza del quale esso si verifica.
PROBLEMA 2
Nella figura 1 è rappresentato il grafico Γ della funzione continua ?:[0, +∞) → ℝ, derivabile in ]0, +∞), e sono indicate le coordinate di alcuni suoi punti.
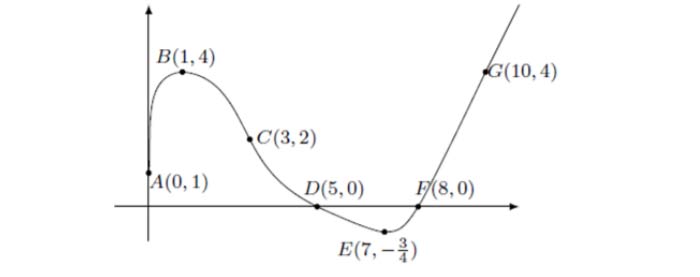
È noto che Γ è tangente all’asse ? in ?, che ? ed ? sono un punto di massimo e uno di minimo, che ? è un punto di flesso con tangente di equazione 2? + ? − 8 = 0.
Nel punto ? la retta tangente ha equazione ? + 2? − 5 = 0 e per ? ≥ 8 il grafico consiste in una semiretta passante per il punto ?. Si sa inoltre che l’area della regione delimitata dall’arco ????, dall’asse ? e dall’asse ? vale 11, mentre l’area della regione delimitata dall’arco ??? e dall’asse ? vale 1.
- In base alle informazioni disponibili, rappresenta indicativamente i grafici delle funzioni ? = ?′(?) ?(?) = ∫ ?(?)?? – con estremi di integrazione 0 e x – Quali sono i valori di ? ′ (3) e ? ′ (5)? Motiva la tua risposta.
- Rappresenta, indicativamente, i grafici delle seguenti funzioni: ? = |?′(?)| ? = |?(?)|′ ? = 1 ?(?) specificando l’insieme di definizione di ciascuna di esse.
- Determina i valori medi di ? = ?(?) e di ? = |?(?)| nell’intervallo [0,8], il valore medio di ? = ?′(?) nell’intervallo [1,7] e il valore medio di ? = ?(?) nell’intervallo [9,10].
- Scrivi le equazioni delle rette tangenti al grafico della funzione ?(?) nei suoi punti di ascisse 0 e 8, motivando le risposte.
Questionario
1. È noto che
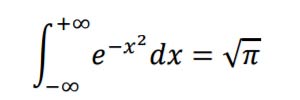
Stabilire se il numero reale ?, tale che
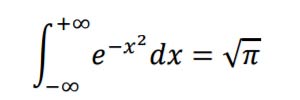
è positivo oppure negativo. Determinare inoltre i valori dei seguenti integrali, motivando le risposte:
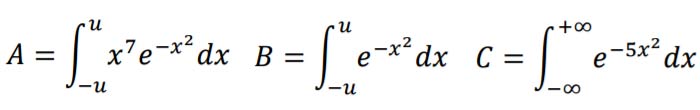
2. Data una parabola di equazione ? = 1 − ?? 2 , con ? > 0 si vogliono inscrivere dei rettangoli, con un lato sull’asse x, nel segmento parabolico delimitato dall’asse x. Determinare ? in modo tale che il rettangolo di area massima sia anche il rettangolo di perimetro massimo.
3. Un recipiente sferico con raggio interno ? è riempito con un liquido fino all’altezza ℎ. Utilizzando il calcolo integrale, dimostrare che il volume del liquido è dato da: ? = ? ∙ (?ℎ2 − ℎ3/3 ).
4. Un test è costituito da 10 domande a risposta multipla, con 4 possibili risposte di cui solo una è esatta. Per superare il test occorre rispondere esattamente almeno a 8 domande. Qual è la probabilità di superare il test rispondendo a caso alle domande?
5. Una sfera, il cui centro è il punto ?(−2, −1, 2), è tangente al piano Π avente equazione 2? − 2? + ? − 9 = 0. Qual è il punto di tangenza? Qual è il raggio della sfera?
6. Si stabilisca se la seguente affermazione è vera o falsa, giustificando la risposta: “Esiste un polinomio ?(?) tale che: |?(?) − cos(?)| ≤ 10−3 , ∀? ∈ ℝ”.
 7. Una pedina è collocata nella casella in basso a sinistra di una scacchiera, come in figura. Ad ogni mossa, la pedina può essere spostata o nella casella alla sua destra o nella casella sopra di essa. Scelto casualmente un percorso di 14 mosse che porti la pedina nella casella d’angolo opposta A, qual è la probabilità che essa passi per la casella indicata con B?
7. Una pedina è collocata nella casella in basso a sinistra di una scacchiera, come in figura. Ad ogni mossa, la pedina può essere spostata o nella casella alla sua destra o nella casella sopra di essa. Scelto casualmente un percorso di 14 mosse che porti la pedina nella casella d’angolo opposta A, qual è la probabilità che essa passi per la casella indicata con B?
(confronta l’immagine a destra)
8. Data la funzione ?(?) definita in ℝ, ?(?) = ??(2? + ?2 ), individuare la primitiva di ?(?) il cui grafico passa per il punto (1, 2?).
9. Date le rette:
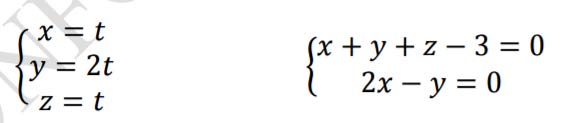
e il punto ?(1, 0, −2) determinare l’equazione del piano passante per P e parallelo alle due rette.
10. Sia ? la funzione così definita nell’intervallo ]1, +∞):
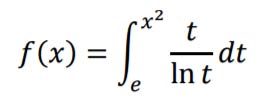
Scrivere l’equazione della retta tangente al grafico di ? nel suo punto di ascissa √?.
Durata massima della prova: 6 ore.
È consentito l’uso della calcolatrice non programmabile.
È consentito l’uso del dizionario bilingue (italiano-lingua del paese di provenienza) per i candidati di madrelingua non italiana.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.
Soluzioni seconda prova maturità 2016
Svolgimento problema 1
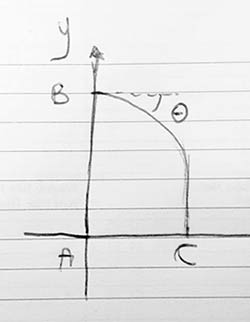
Per poter iniziare ad affrontare questo problema di maturità 2016, è necessario fissare un sistema di riferimento. Un origine degli assi cartesiani nel punto A come ci viene suggerito dalla traccia. Per cui possiamo subito dare le coordinate cartesiane di alcuni punti:
 A(0,0)
A(0,0)
B(0,1)
Dato che la figura è simmetrica rispetto all’asse delle ordinate, possiamo studiarne solo metà, cioè per x compreso nell’intervallo [0;1]. Notiamo che il punto di intersezione che chiamiamo C della curva con l’asse delle ascisse ha coordinate (1,0) dato che la lunghezza totale del serbatoio è 2 metri.
Quello che notiamo è che in B deve esserci un punto angoloso, per cui la derivata della funzione nel punto di ascissa 0 deve essere diversa da zero. Cioè f ‘ (0) diverso da 0.
Per questa ragione possiamo subito scartare la funzione f3 che ci viene proposta dalla traccia. Facendone la derivata otterrei il seno di qualcosa. Sostituendo 0 al posto della x otterrei il seno di 0, e quindi la funzione derivata prima in quel punto sarebbe nulla. Ciò non sarebbe compatibile con la figura e quindi possiamo scartare questa terza soluzione.
Altro dato che ci viene fornito dalla traccia è che la funzione passi sia per B che per C. Quindi sostituendo in f2 le coordinate di B(1;0) e C(0;1) deve uscire un’identità (del tipo un numero uguale a se stesso). Proprio per questa ragione possiamo escludere anche la seconda soluzione. Inoltre facendone la derivata seconda, otterrei un profilo concavo/convesso differente da quello suggerito dalla figura. Infatti:
f ” (x) = -36x+18
Facendo il calcolo di concavità e convessità -36x>-18 → x<1/2. Significa che in corrispondenza dell’ascissa x=1/2 dovrei avere un cambiamento di concavità. Cosa incompatibile con la figura. Per questa ragione la soluzione al punto 1 del problema 1 è f1. Cioè la funzione f1 rappresenta il grafico in figura.
Per rispondere al punto 2, occorre calcolare il volume del serbatoio. Per effettuare questo calcolo moltiplichiamo l’area della sezione trasversale (che chiamiamo S) per la lunghezza del serbatoio (L=8) → V= S · L
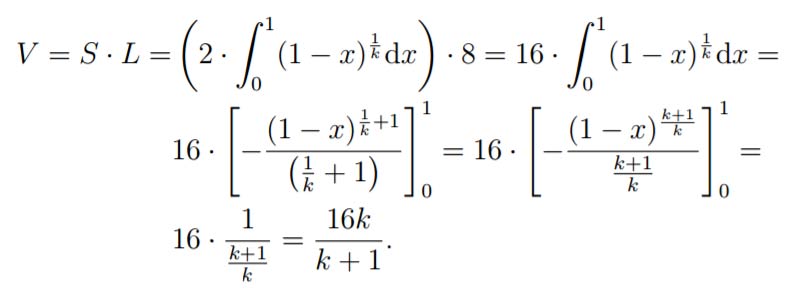
Il volume, così come ce lo chiede la traccia deve essere almeno di 13 metri cubi. Per cui imponiamo la disuguaglianza…
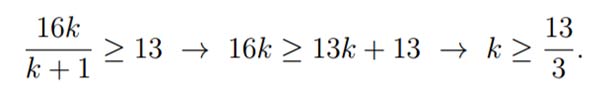
Poiché K deve essere compreso tra 1 e 5 e allo stesso tempo deve essere maggiore di 13/3 (cioè di 4,3), allora possiamo scrivere che k=5. Per k=5 il volume diventa V=(16*5)/(5+1)= circa 13,3 metri cubi che è maggiore dei 13 metri cubi richiesti.
A questo punto possiamo calcolare il punto 3 del problema 1 della maturità 2016.
Bisogna calcolare il volume individuando una funzione V(z) che associa il livello di gasolio nel serbatoio la percentuale di riempimento del Volume da indicare sul serbatoio stesso.
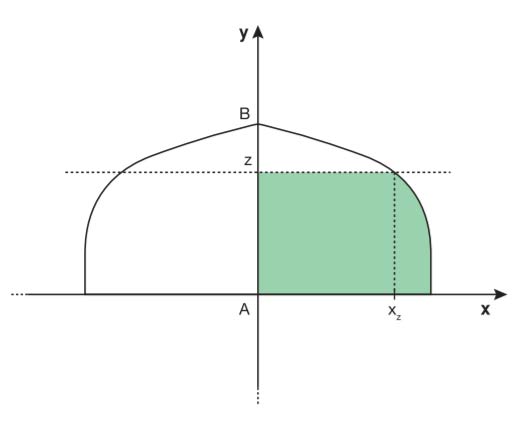
Immagine Zanichelli editore
Fissata x l’ascissa possiamo trovare che:
z=(1-x)1/5
da cui possiamo ricavare la x
x=1-z5
Il volume di gasolio contenuto nel serbatoio è:
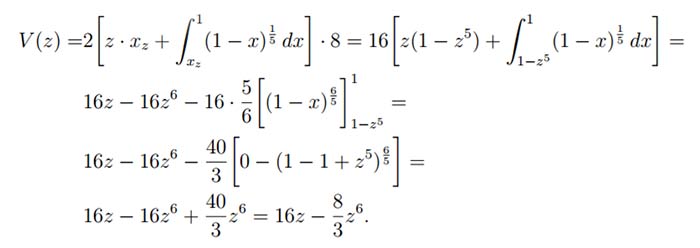
A questo punto possiamo calcolare la percentuale di serbatoio riempito come il volume in funzione di z fratto il volume totale.
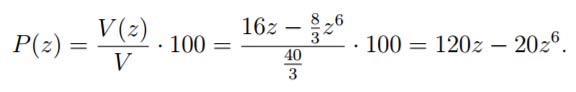
Per risolvere l’ultimo punto, possiamo dire che abbiamo trovato k=5. Quando z=50cm, cioè mezzo metro, allora
P(0,5m)=120(0,5)- 20 x (0,5)6 =59,7 %
Il riempimento proposto del 50% è quindi sbagliato, poiché il volume individuato non è rettangolare ma ha una forma irregolare che lo porta ad essere più capiente verso la base. L’amministrazione propone invece di usare la formula:
P(a)= 100z
La differenza tra P(z) e P(a) è pari a d(z)=120z-20z6-100z=20z-20z6
Si calcola il massimo della funzione d(z) cioè d'(z)=20-120z5, continuando come si fa lo studio di funzione, si pone derivata prima uguale e poi maggiore di 0.
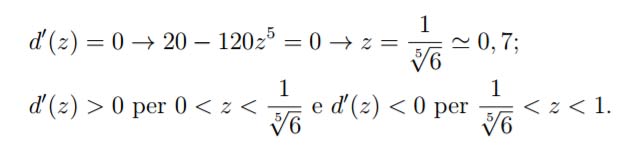
Per cui l’errore massimo si ha in corrispondenza di z=0,7m.
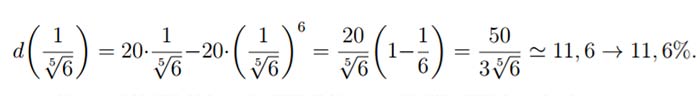
Esercizio 2 + quesiti in fase di caricamento…