Uno degli esercizi più difficili di tutto il programma di geometria analitica è la retta tangente alla circonferenza passante per un punto. Vediamo come risolvere questo tipo di esercizio in maniera semplice e senza commettere errori.
Indice
- Spiegazione dell’esercizio e della traccia
- Guarda come si risolve con un esempio
- Tracce ed esercizi da risolvere
Spiegazione dell’esercizio e della traccia
Determinare l’equazione della retta tangente alla circonferenza e passante per il punto P di coordinate note. Generalmente è questa la traccia che viene proposta e che mette in difficoltà gli studenti. L’esercizio sostanzialmente ci sta chiedendo di calcolare l’intersezione tra una retta e una circonferenza, soltanto che la retta non la conosciamo ancora. Ovviamente la condizione di tangenza si traduce con il fatto che le due curve hanno un solo punto di intersezione.
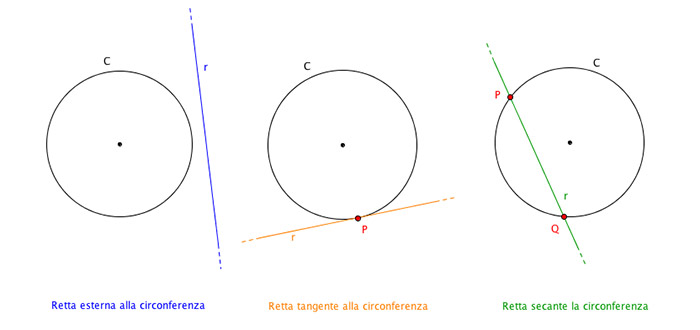
La condizione di tangenza si esprime indicando l’esistenza di un solo punto in comune
Come si risolve questo esercizio? Innanzitutto sappiamo che l’equazione della retta è y=mx+q, ma passa anche per un punto. Per cui applichiamo la formula della retta passante per 1 punto, per cui le incognite non saranno più m e q, ma soltanto m. Il coefficiente angolare resta infatti l’unica vera incognita del problema.
A questo punto calcoliamo l’intersezione tra la retta con incognita m e la circonferenza data dalla traccia dell’esercizio. Poiché i punti in comune non sono due, mi aspetto di avere non 2 soluzioni, ma soltanto 1. Per cui quando risolvo il sistema e mi trovo a dover calcolare il delta nell’equazione di secondo grado, devo imporre la condizione DELTA = 0.
Otterrò così un’equazione in cui l’unica incognita è il coefficiente angolare. Risolvendola ho ottenuto m, che posso sostituire nell’equazione della retta e l’esercizio è risolto.
Esercizio svolto sulla retta tangente alla circonferenza
Determinare le equazioni delle rette tangenti alla circonferenza x2+y2-2x+4y+1=0 e passante per il punto P(5;3).
Innanzitutto ai fini del calcolo non ci interessa sapere che il punto P appartenga o meno alla circonferenza. La cosa importante è che la retta passi per quel punto. Utilizziamo quindi subito l’equazione della retta passante per 1 punto. y-yp=m(x-xp).
Otteniamo quindi la retta y-5=m(x-3), che dopo un semplice passaggio diventa y=mx-3m+5. A questo punto possiamo andare a scrivere il sistema così da calcolare la retta tangente alla circonferenza.
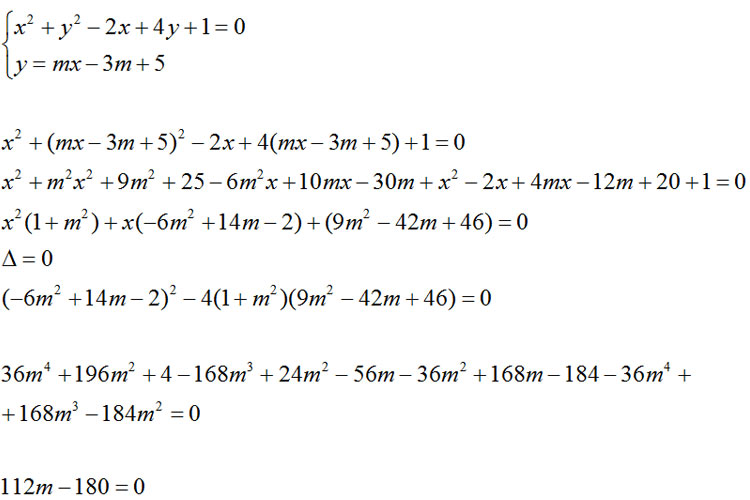
Ho ottenuto una semplice equazione di primo grado dove l’incognita è la m, ovvero il coefficiente angolare della retta tangente alla circonferenza. In particolare dopo i calcoli ottengo m=45/28. A questo punto basta andare a sostituire nell’equazione della retta iniziale e siamo riusciti a risolvere l’esercizio in maniera semplice.
y=mx-3m-5, diventa cioè y=45/28 x – 107/28.
Tracce ed esercizi da risolvere
Se stai cercando qualche altro esercizio sulle rette tangenti alla circonferenza ti suggeriamo alcune tracce su cui esercitarti.
- Determinare l’equazione della retta tangente alla circonferenza x2+y2+6x+4y-8=0 e passante per il punto P(4;-1)
- Determinare la retta tangente alla circonferenza di equazione x2+y2+4x-2y+4=0 e passante per il punto P((5,4)