In questa lezione vedremo la razionalizzazione del denominatore di una frazione. Imparerai così a risolvere i tuoi esercizi di matematica senza più temere le radici.
Argomenti della lezione
A che serve?
Razionalizzazione di un monomio
Razionalizzazione di un binomio
Esercizi svolti
A che serve la razionalizzazione di radicali?
Nelle scorse lezione hai potuto studiare le regole e le proprietà dei radicali, imparando a risolvere le operazioni fondamentali anche grazie ad esercizi svolti. Non abbiamo ancora visto il caso in cui abbiamo una frazione con al denominatore un radicale.
Affronteremo il discorso in maniera molto più complessa nelle lezioni sulle equazioni irrazionali. Per ora ci basti sapere che la razionalizzazione del denominatore di una frazione serve a fare in modo che il suo denominatore non contenga radici.
I metodi di razionalizzazione sono sostanzialmente due e riguardano la presenza, al denominatore, di un monomio o di un binomio. Analizziamoli assieme…
Razionalizzazione del denominatore con un monomio
Il caso più semplice si presenta quando il denominatore irrazionale è un monomio, cioè quando nella frazione compare un’unico elemento sotto radice. In questo caso è sufficiente moltiplicare numeratore e denominatore per un radicale conveniente, come negli esempi che ti mostriamo:

La razionalizzazione della radice quadrata è il caso più semplice: basta riscrivere la frazione moltiplicando e dividendo per la stessa radice. Alla fine ci ritroviamo con un risultato in cui la radice quadrata non appare più nel denominatore.
Ciò che a scuola non ci insegnano, o che spesso alla lavagna non viene capito, è come fare la razionalizzazione di una radice cubica, in quanto non è sufficiente moltiplicare e dividere per la radice. Vediamo subito un esempio concreto:
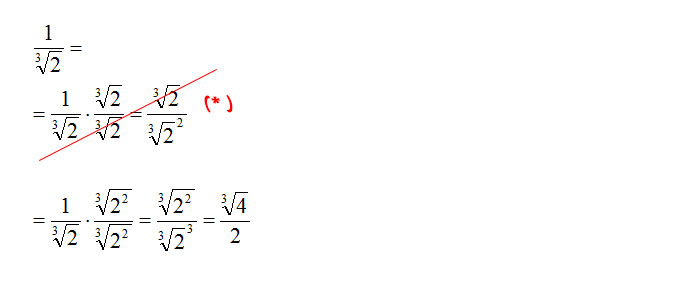
(*) Svolgendo la razionalizzazione della radice cubica come nel caso della radice quadrata il risultato finale non mi porta ad eliminare il radicale dal denominatore. Il modo più semplice per razionalizzare, in questo caso è far in modo che il denominatore abbia un esponente pari all’indice di radice. Quindi 2 (sottinteso elevato a 1) deve diventare elevato a 3 dato che l’indice di radice è 3. Questo significa che va moltiplicato con esponente 2.
Vediamo un altro esempio sulla razionalizzazione di una radice cubica.
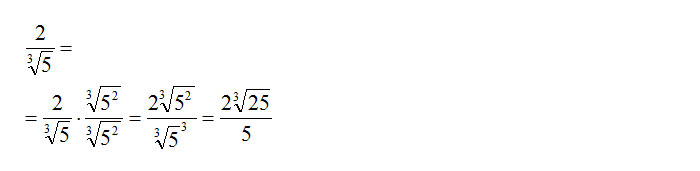
Esempio di razionalizzazione di una radice cubica
Razionalizzazione del denominatore con un binomio
Se il denominatore è un binomio, basta moltiplicare numeratore e denominatore per lo stesso binomio, ma col secondo termine cambiato di segno, ricordando la regola dei prodotti notevoli:

Ricordi la regola dei prodotti notevoli?
Per capire meglio come si fa la razionalizzazione con il binomio, risolviamo subito qualche esercizio assieme:
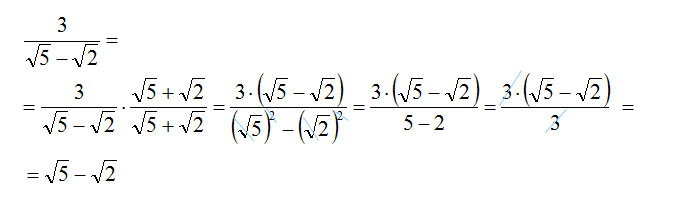
Denominatore con binomio
Nulla di difficile: abbiamo due radici che si sommano al denominatore (nel nostro caso si sottraggono). E’ stato sufficiente moltiplicare e dividere per lo stesso binomio cambiando semplicemente il segno del secondo. Facciamo poi le semplificazioni e ci ritroviamo il risultato senza radicale al denominatore.
Esercizi sulle razionalizzazioni di radicali
Capito come si razionalizza una radice nei due metodi illustrati, proviamo a risolvere assieme alcuni esercizi. La traccia ci chiede di eseguire, per ogni esercizio, la razionalizzazione del denominatore con i metodi visti. Iniziamo subito:
Rendere razionali i denominatori delle seguenti frazioni
-
-
- In questo primo esercizio quale dei due metodi di razionalizzazione usiamo? Ovviamente il primo perché siamo in presenza di un monomio. Ecco come risolvere in pochi semplici passaggi:

- Il secondo esercizio riguarda le razionalizzazioni dei radicali cubici. Anche questo esempio ci conferma come non esista una regola specifica se non quella di fare in modo che esponente ed indice di radice coincidano. Vediamo come:

Abbiamo fatto in modo che la radice cubica di b al quadrato diventasse radice cubica di b al cubo. Solo così infatti possiamo semplificare e riusciamo ad eliminare i radicali al denominatore.
- Nell’ultimo esercizio svolto eseguiamo una razionalizzazione del denominatore di una frazione con un binomio.

- In questo primo esercizio quale dei due metodi di razionalizzazione usiamo? Ovviamente il primo perché siamo in presenza di un monomio. Ecco come risolvere in pochi semplici passaggi:
-
Per altri esercizi ti rimandiamo all’Esercizio 5 pubblicato dall’Istituto “A. Pacinotti” Fondi. Se hai dubbi o perplessità sulla lezione, o non riesci a risolvere gli esercizi che ti sono stati assegnati a casa dal tuo professore, allora contattaci e cercheremo di aiutarti con ulteriori esempi e dispense.
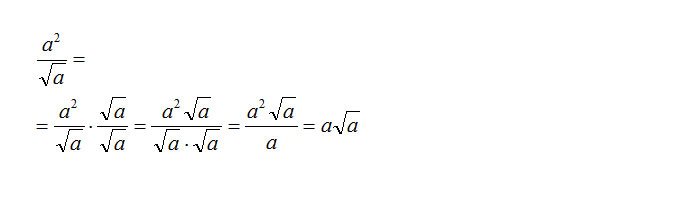
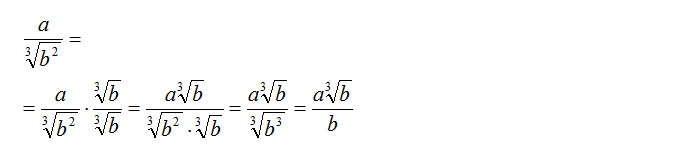
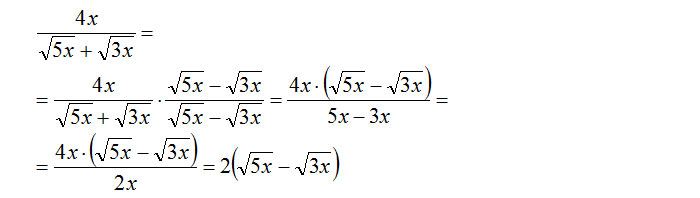
buongiorno, mi risulta esserci un errore nel primo esercizio che riguarda l’applicazione dei prodotti notevoli… Al numeratore è stato erroneamente cambiato il segno…
Grazie Monica,
siamo sempre orgogliosi quando i nostri studenti correggono sviste o errori presenti nelle varie lezioni pubblicate. E’ anche grazie a te se riusciamo a rendere gli appunti sempre più precisi e facili da consultare.
Continua a seguirci