Il calcolo del massimo comune divisore è uno degli argomenti più importanti di tutto il programma di algebra, così come il minimo comune multiplo (mcm). In questa lezione ti mostreremo come calcolare mcd in modo semplice e seguendo pochi semplici passaggi. Riuscirai con questa nostra breve regola a risolvere gli esercizi di matematica e di algebra più complessi.
Il calcolo di mcd, che all’inizio potrà sembrarti impegnativo, con il passare del tempo diventerà così automatico che riuscirai addirittura a calcolare il massimo comune divisore a mente, meglio di un calcolatore!
Sostanzialmente riuscirai a trovare un numero, partendo da quelli che ti assegna la traccia, che può essere il divisore di tutti. Ma non complichiamoci la vita da subito e facciamo un passo alla volta.
A che serve il massimo comune divisore
Prima di vedere la regola per calcolare il massimo comune divisore è importante che tu sappia che questo potente strumento ti servirà non solo nel calcolo delle frazioni negli esercizi sul m.c.d., ma anche negli esercizi sui monomi e sui polinomi.
In particolar modo studierai il raccoglimento a fattore comune che si basa interamente sul calcolo del mcd, su alcuni testi chiamato anche minimo comune divisore.
Definizione di massimo comune divisore
Iniziamo cercando di capire qual è la definizione del mcd, ovvero che cos’è il massimo comune divisore. In tutti i libri di matematica che si usa a scuola viene enunciata la seguente regola.
Per il calcolo del mcd si prendono i fattori comuni presi una sola volta con il minimo esponente.
Si tratta di una definizione che nella matematica ritornerà molto spesso e non solo con le frazioni, tanto che la imparerai presto a memoria. Vediamo qual è il significato di questa definizione per poter ottenere così una regola, cioè un metodo che ci permetta di capire come calcolare il massimo comune divisore. Facciamo subito un esempio pratico, così da eliminare tutti i dubbi e le difficoltà.
- Calcolare il mcd dei seguenti numeri: 10;15;100.
La definizione ci dice di dover prendere i fattori comuni. Questo significa che il primo step è quello di dividere i vari numeri datici dalla traccia in fattori, cioè in numeri primi. Per il calcolo del mcd prenderemo, tra questi, solo quelli comuni a tutti e con il minimo esponente.
Nel nostro caso, cioè, 10=2x5, 15=3x5, 100=2^2x5^2. Dei vari fattori primi che abbiamo ottenuto scomponendo i numeri della traccia, solo 5 è quello che compare sempre e va preso con il minimo esponente. Per cui il massimo comune divisore dei numeri dati è 5.
NOTA BENE: se non ci sono elementi comuni tra i vari fattori, il massimo comune divisore è 1.
Calcolo mcd – esempio svolto
Non ti è ancora chiaro e non hai capito oppure vorresti un altro esempio per togliere i dubbi che ti sono rimasti? Ebbene nell’esercizio svolto sul mcd che ti proponiamo ora ti mostriamo tutti gli step anche con delle immagini. Così ti facciamo vedere non solo come si calcola mcd ma anche esattamente cosa dovrai scrivere sul tuo quaderno quando farai gli esercizi.
Il metodo di calcolo che ti facciamo vedere è valido per tutti: come aiuto dislessia, per la scuola primaria, media o superiori. Tutti possono applicare questa regola così da rendere tutto più semplice. Ecco la traccia dell’esercizio.
- Calcolare il massimo comune divisore di 50, 10 e 30.
Quello che ti proponiamo è un metodo a step infallibile, leggilo attentamente. E’ facile e noi cercheremo di essere chiari e di esportelo in modo semplice così che possa tu usare questa regola anche nei tuoi esercizi.
- STEP 1 – Scomporre i 3 numeri in fattori primi.
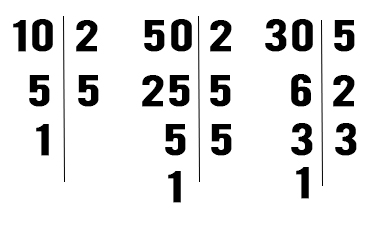
- STEP 2 – Riscrivo ogni numero come uguale alla moltiplicazione dei fattori individuati su ogni colonna destra.
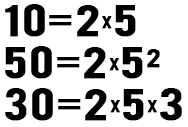
- STEP 3 – Cerchio tutti i numeri a destra dell’uguale che compaiono in tutte le righe che abbiamo scritte. In questo caso sia il 5 che il 2 sono sempre presenti.

- STEP 4 – Di quelli evidenziati, per calcolare il mcd, considera quelli con l’esponente più basso. Tra 5 (che corrisponde a 5^1) e 5^2, andremo a considerare il primo. Il mcd sarà la moltiplicazione di questi numeri (presi una sola volta)
mcd=2×5=10
Questo vuol dire che il massimo comune divisore tra 50, 10 e 30 è 10.
Esercizi da svolgere
Ti abbiamo dato così una regola per calcolare il massimo comune divisore. Sei pronto quindi per provare se hai capito con degli esercizi facili. Ecco le tracce degli esercizi con risultati sul mcd.
- Calcolare il massimo comune divisore tra 12 e 18 (Risultato: mcd=6)
- Calcolare il massimo comune divisore tra 26 e 42 (Risultato: mcd=2)
- Calcolare il massimo comune divisore tra 40 e 70 (Risultato: mcd=10)
- Calcolare il massimo comune divisore tra 15, 6 e 10 (Risultato: mcd=2)
- Calcolare il massimo comune divisore tra 9, 24 e 6 (Risultato: mcd=3)
Per dubbi o chiarimenti il nostro staff è a tua disposizione. Contattaci per avere una mano con i tuoi esercizi di matematica.