Per distanza punto retta si intende la formula grazie alla quale è possibile calcolare la distanza di un punto da una retta in geometria analitica. Per poterla applicare sono necessari:
- le coordinate di un punto P
- l’equazione della retta r.
Definizione
Ecco alcune definizioni che si trovano sui libri di testo. Puoi scegliere quella che ritieni più semplice.
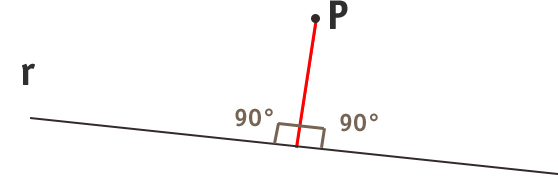
- La distanza punto retta è la misura del segmento che dal punto P cade perpendicolarmente sulla retta r.
- La distanza di un punto da una retta è la dimensione del proiezione ortogonale del punto P sulla retta r.
- E’ la distanza minima tra il punto P e tutti i punti appartenenti alla retta r.
d(P,r)=min{d(P,R), con R∈r}
Distanza punto retta formula
In geometria analitica tutto ciò si traduce in una semplice formula. Dati quindi:
- un punto di coordinate P(xP,yP);
- l’equazione della retta implicita r: ax+by+c=0
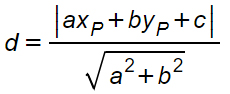
Quini la distanza di un punto da una retta si calcola facendo il valore assoluto della somma dei prodotti delle coordinate dei punti per i coefficienti della retta, fratto la radice quadrata della somma dei quadrati dei coefficienti della retta.
Alcuni suggerimenti
- assicurati che l’equazione della retta sia nella forma implicita (cioè al secondo membro devi avere 0). Se il problema dovesse darti la forma esplicita, ricordati di trasformarla in implicita prima di calcolare la distanza punto retta.
- il valore assoluto rende il numeratore positivo, per cui la misura della distanza sarà sempre un valore positivo. Se ci pensi è anche normale: come fanno due oggetti ad essere distanti tra loro ad esempio -100 metri?
- applica la formula distanza aiutandoti con delle parentesi. Eviterai di fare degli errori riportando i segni.
Distanza punto retta dimostrazione
La dimostrazione della formula della distanza di un punto da una retta non è particolarmente complessa, ma si basa su quanto già studiato in precedenza. In genere non viene richiesta a lezione, ma la riportiamo per completezza per chiunque voglia approfondire.
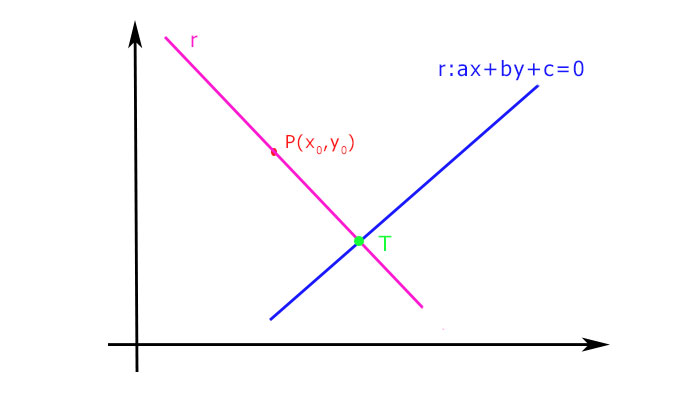
Come procediamo? Sintetizziamo per punti:
- La distanza punto retta è il segmento in figura indicato con PT. Considerando che P è un dato della traccia, posso trovare le coordinate del punto P attraverso l’intersezione tra le due rette r e r’ (quella in viola e quella in blu).
- Poiché r viene data dalla traccia, devo poter calcolare r’ (in viola). Noto che questa passa per P ed è perpendicolare ad r (in blu). Questo perché la distanza punto retta è un segmento perpendicolare alla retta stessa.
- Posso quindi calcolare r in viola come retta passante per un punto e con coefficiente angolare pari a m’=-1/m
Approfondimenti: il coefficiente angolare nelle rette perpendicolari
Iniziamo quindi a scrivere la formula della retta passante per un punto:
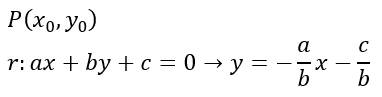
A questo punto imponiamo la condizione di perpendicolarità, per cui:
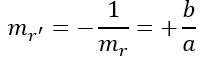
Possiamo a questo punto scrivere la formula della retta in viola r’.
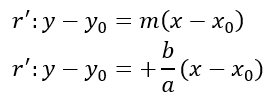
Poiché a, b, x0 e y0 sono noti, abbiamo così calcolato l’equazione della retta. Possiamo quindi intersecare le due rette per trovare T, scrivendo il sistema di equazioni:
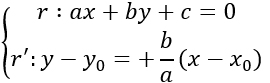
In questo modo possiamo trovare x e y, ovvero le coordinate del punto T. Basta a questo punto trovare la distanza tra i due punti PT e abbiamo risolto il problema.
Esercizi svolti
Esercizio 1
Calcolare la distanza punto-retta dove P(2,3) e r:x+y-1=0
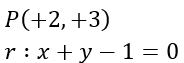
Questo primo esempio è particolarmente semplice, visto che basta applicare la formula vista sopra:
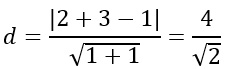
Teoricamente l’esercizio potrebbe essere già concluso, ma dalle regole sui radicali sappiamo che è necessario rimuovere la radice quadrata dal denominatore, per cui dobbiamo eseguire la razionalizzazione, per cui moltiplico e divido per la radice di 2.
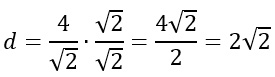
L’esercizio n.1 è abbastanza banale, basta sostituire i dati nella formula vista in alto e il problema è risolto. Nella parte finale, vi abbiamo ricordato come si fa a razionalizzare una radice quadrata. Se dovessero esserci problemi su questi calcoli, ti consigliamo di riguardarti la lezione sulle radici.
- Calcolare la distanza di P(4,3) da r:y=2x-3 -> PROVA A RISOLVERLO COME ESERCIZIO PER CASA
SUGGERIMENTO: In questo secondo esercizio parti dall’equazione in forma esplicita della retta e trasformala in implicita. In questo modo ti riconduci al caso precedente, per cui abbiamo individuato la distanza punto-retta.
Esercizio 2
Calcola la distanza del punto P(0;6) dalla retta che passa per i punti A(2,3) e B(1/2;1)
Quello che si può subito notare è che la traccia ci chiede di calcolare la distanza tra punto e retta, ma non ci fornisce direttamente quest’ultima. Sappiamo solo che la retta r passa per i punto A e B. Quindi la prima operazione è quella di utilizzare la retta passante per 2 punti.
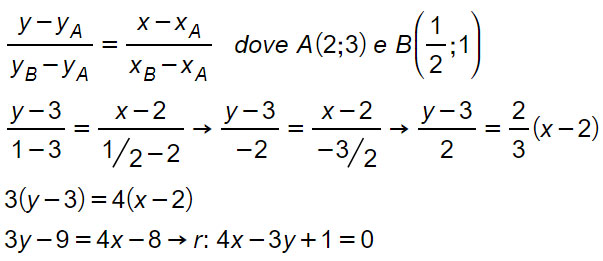
A questo punto, avendo calcolato la retta, possiamo utilizzare le conoscenze apprese oggi. In particolare:
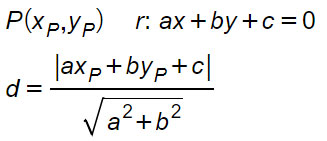
Andiamo ad applicare la formula al nostro esercizio, per ottenere quindi:
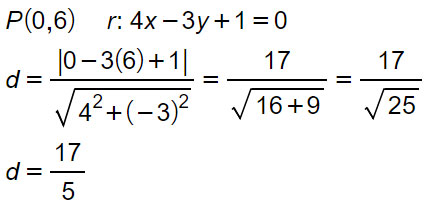
Ti è piaciuta la lezione? Hai ancora dei dubbi? Non riesci a capire un passaggio? Lascia un commento a fondo pagina. I tuoi commenti ci aiuteranno a migliorare e a offrirti ogni giorno contenuti di qualità.