In questa breve lezione vedremo come risolvere le disequazioni esponenziali. Nella prima parte analizzeremo, con pochi pratici suggerimenti, le regole che vengono dalla teoria, così da concentrarci poi solo su esempi ed esercizi svolti.
Come si risolvono?
A scuola non le hai capite ed ora ti ritrovi costretto a far i conti con degli esercizi che non sai risolvere… Niente paura: ti daremo in pochi semplici passaggi un aiuto sulle disequazioni irrazionali. In questo modo potrai risolvere espressioni ed esercizi di matematica anche più difficili ed in pochi minuti. Iniziamo però con calma…
Le disequazioni esponenziali e logaritmiche si svolgono più o meno nello stesso modo: il principio che ti aiuterà a risolvere gli esercizi anche più difficili sono praticamente gli stessi. Per questa lezione è fondamentale che tu abbia già studiato le equazioni esponenziali o almeno tu sappia che cos’è la funzione esponenziale stessa.
Come quasi sempre accade, la regola generale è cercare di ricondurci alla forma base:
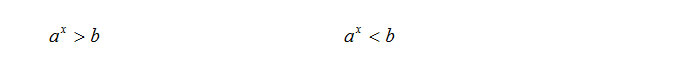
Nel caso in cui b (cioè il numero al secondo membro) è minore di 0, allora nel primo caso ho una disequazione sempre verificata (scriveremo con simboli “per ogni x appartenente a R”), mentre nel secondo caso una disequazione impossibile.
Questo perché a elevato a x deve necessariamente essere positivo per definizione di esponenziale. Ricordando che la funzione esponenziale è crescente quando la base è maggiore di zero, decrescente quando la base è compresa tra 0 e 1, allora dobbiamo distinguere due diversi casi:
-
se 0<a<1, allora:
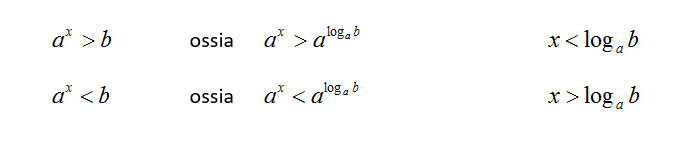
-
se a>1
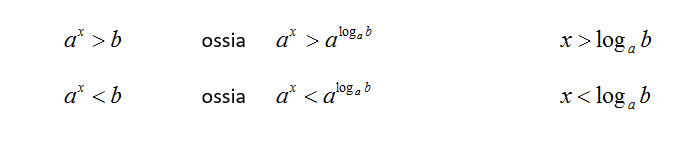
Trucchi e suggerimenti che ti vengono in aiuto
Dal punto di vista teorico la lezione potrebbe anche essere finita qui. La cosa che ci preme che tu abbia capito è che, quando la base dell’esponenziale è minore di 1 dovrai ricordarti di invertire il verso della disequazione. Quando invece la base dell’esponente è maggiore di 1 non dovrai farti alcun tipo di problema e risolvere normalmente.
Esercizi ed esempi svolti sulle disequazioni esponenziali
Risolviamo i seguenti esercizi sulle disequazioni esponenziali.

Negli esercizi facili, come il primo che ti abbiamo proposto, non è necessario neanche fare il passaggio ai logaritmi. Semplicemente è stato sufficiente ricordarci le proprietà delle potenze e trasformare 16 in una potenza con lo stesso esponente.
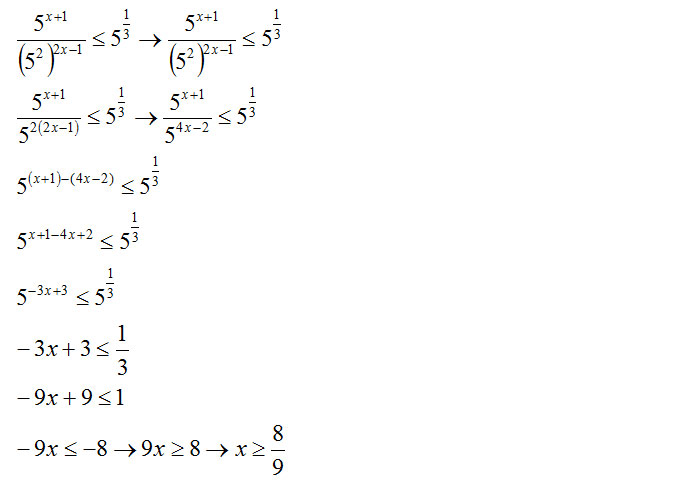
Il secondo esercizio che hai visto è uno delle più semplici disequazioni esponenziali fratte. Anche in questo caso infatti non abbiamo usato le radici, ma le proprietà delle potenze e, alla fine, un facile minimo comune multiplo per la presenza della frazione 1/3.
In questo caso abbiamo risolto degli esercizi con le basi uguali. Nel momento in cui ci troviamo a dover risolvere delle disequazioni esponenziali con basi diverse, dovremo necessariamente fare ricorso ai logaritmi.
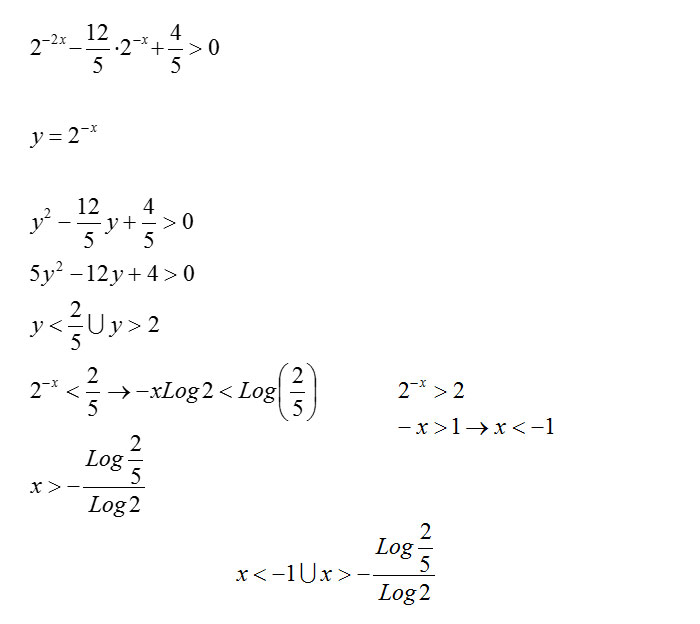
In quest’ultimo esercizio abbiamo dovuto provare a risolvere la disequazione esponenziale con due incognite: la seconda ci è infatti servita per semplificarci il problema trasformando il tutto in una banale disequazione di secondo grado. A quel punto abbiamo trasformato la disequazione esponenziale attraverso i logaritmi ed ottenuto in seguito il risultato finale.
Se vuoi ancora esercitarti ti consigliamo questo PDF, è tratto da un buon eserciziario usato al liceo scientifico.