Disequazioni di secondo grado: spiegazione e schema risolutivo

Le disequazioni di secondo grado sono delle disequazioni in cui l’incognita compare con un esponente al quadrato. In questa lezione vedremo che cosa sono le disequazioni di secondo grado, come si risolvono e quali sono i vari tipi di esercizi che possono capitare durante un compito.

Per capire come si risolvono le disequazioni di secondo grado è importante che tu abbia studiato, e quindi capito, le equazioni di secondo grado, perché anche in questo caso andremo a trovare due soluzioni x₁ e x₂. La soluzione però sarà data da un intervallo di valore. Iniziamo però con calma e capiamo subito cosa sono e come si presenta una disequazione di secondo grado.

ax²+bx+c>0
ax²+bx+c≥0
ax²+bx+c<0
ax²+bx+c≤0

Queste che hai visto elencate sono le quattro forme in cui si possono presentare le disequazioni di secondo grado. Abbiamo un termine al quadrato, un termine di primo grado e quello che viene chiamato termine noto. Il verso può essere maggiore, minore, maggiore e uguale o minore e uguale.

Dei tre coefficienti, a ovviamente deve essere diverso da zero, altrimenti avremmo il caso di una disequazione di primo grado.

ax²+bx+c>0 → a=0 → bx+c=0 → x=-b/c

Come fare per risolvere disequazioni di II grado

Molti testi di matematica propongono metodi e tecniche risolutive differenti. Noi ti proponiamo in questa lezione quella più facile e sicura, cioè che richiede meno sforzi mentali e presenta meno rischi di errori.

1 – Assicurati che a>0

Per non complicare troppo gli esercizi, fai in modo che il primo coefficiente sia positivo. Se dovessi vedere un segno meno, cambia tutti i segni e il verso della disequazione.

2 – Calcola le due soluzioni

Fai finta almeno per questo momento che stai risolvendo un’equazione di secondo grado e usa le formule risolutive che conosci, come ad esempio la formula del delta. Sui libri di testo troverai scritto che per risolvere le disequazioni di secondo grado, bisogna passare all’equazione associata. Cioè:

ax²+bx+c>0 → ax²+bx+c=0

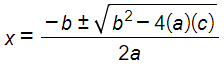
3 – Schema risolutivo

A questo punto abbiamo calcolato x₁ e x₂ e si possono presentare i seguenti casi:

•  x₁ = x₂ (quindi Δ=0)

  • Nella disequazione c’è maggiore (>) → ax²+bx+c>0 → Soluzione: la disequazione è sempre verificata, tranne i due valori in cui la disequazione di II grado si annulla, cioè scriverò ∀x∈R, x≠x₁
  • Nella disequazione c’è maggiore e uguale (≥) → ax²+bx+c≥0 → Soluzione: la disequazione è sempre verificata, cioè scriverò ∀x∈R
  • Nella disequazione c’è minore (<) → ax²+bx+c<0  → Soluzione: la disequazione non è mai verificata.
  • Nella disequazione c’è minore e uguale (≤) → ax²+bx+c≤0 → la disequazione di secondo grado non è mai verificata tranne che per i valori x=x₁

• x₁ ≠ x₂ (quindi Δ>0)

• • • Nella disequazione c’è maggiore (>) → ax²+bx+c>0 → Soluzione: x<x₁ U x>x₂
    • Nella disequazione c’è maggiore e uguale (≥) → ax²+bx+c≥0 → Soluzione: x≤x₁ U x≥x₂
    • Nella disequazione c’è minore (<) → ax²+bx+c<0  → Soluzione: x₁<x<x₂
    • Nella disequazione c’è minore e uguale (≤) → ax²+bx+c≤0 → x₁≤x≤x₂

• Non ci sono soluzioni reali (quindi Δ<0)

• • Nella disequazione c’è maggiore (>) → ax²+bx+c>0 → Soluzione: la disequazione è sempre verificata, ∀x∈R.
  • Nella disequazione c’è maggiore e uguale (≥) → ax²+bx+c≥0 → Soluzione: la disequazione è sempre verificata, ∀x∈R.
  • Nella disequazione c’è minore (<) → ax²+bx+c<0  → Soluzione: la disequazione non è mai verificata, MAI
  • Nella disequazione c’è minore e uguale (≤) → ax²+bx+c≤0 → la disequazione non è mai verificata, MAI

Disequazioni di secondo grado spurie

Esistono alcuni casi più semplici dove puoi evitare di fare il calcolo del delta, tra queste le disequazioni di II grado spurie. Esempio:

x²+2x≤0

Passo subito all’equazione associata

x²+2x=0

Noto che manca il termine noto, per cui posso mettere in evidenza la x.

x(x+2)=0

Le soluzioni sono x=0 e x=-2. Analizzando la tabella precedente noto che sono nel caso in cui le due soluzioni sono diverse tra loro e c’è il simbolo minore e uguale. Per cui la soluzione è:

-2≤x≤0

Disequazioni di secondo grado pure

Questo tipo di disequazioni di 2 grado sono le più sbagliate dagli studenti, perché apparentemente le più semplici. Qui bisogna fare molta attenzione al delta negativo. Mi ritrovo infatti di fronte ad una disequazione binomia del tipo:

ax²+c>0

1. 1. Se i coefficienti a e c sono discordi puoi risolvere come una normale equazione di secondo grado pura. Quindi portiamo c al secondo membro, radice quadrata e troviamo le due soluzioni x1 e x2. A questo punto seguo la tabella vista sopra.

1. Se i coefficienti a e c sono concordi, se provassi a usare la formula normale per le equazioni di 2 grado, avresti un delta negativo. Queste disequazioni binomie infatti vanno risolte nel seguente modo:
   1. 1. 3x²+1<0 → IMPOSSIBILE
   1. 3x²+1>0 → ∀x∈R

Col verso minore il risultato è impossibile: questo perché il binomio è sempre positivo e non può essere minore di zero. Quando c’è il verso maggiore il risultato è sempre verificato (cioè per ogni x appartenente a R).

Esempi

Dedicheremo un’intera lezione agli esercizi sulle disequazioni di secondo grado. In questa lezione vedremo solo alcuni esempi per  capire come applicare le formule viste sopra.

Esercizio 1

x²-5x<0

Svolgimento

Questa che ci viene presentata dalla traccia rientra tra le disequazioni di secondo grado spurie. Per cui si fa un raccoglimento totale della x.

x(x-5)<0

L’equazione associata è x(x-5)=0 le cui soluzioni sono x₁=5 e x₂=0

Entro nella tabella con x1 diverso da x2 e con il simbolo minore. Il risultato è per valori compresi. Per cui la soluzione posso scriverla come:

0<x<5.

Esercizio 2

-x²-10x-25<0

Svolgimento

Visto che il primo coefficiente è negativo, invertiamo tutti i segni e il verso della disequazione.

x²+10x+25>0

Passiamo all’equazione di II associata:

x²+10x+25=0 → calcolo il delta → Δ=b²-4ac=100-4(25)=0

x=-10/2=-5

Ho il delta uguale a zero, per cui rientro nel caso in cui le due soluzioni sono uguali tra loro e ho verso maggiore. Per cui la soluzione è:

∀x∈R, x≠-5

Esercizio 3

x²+4x-21>0

Svolgimento

Passiamo all’equazione associata e calcoliamo le due soluzioni.

x²+4x-21>0 → x²+4x-21=0  → x₁=-7 e x₂=3

Siamo nel caso in cui le due soluzioni sono tra loro diverse, mentre il verso è maggiore. Per questa ragione si prendono soluzioni esterne. Il risultato è quindi:

x<-7 U x>3