Trovare l’equazione della circonferenza per tre punti

L’equazione della circonferenza per tre punti si determina andando a creare una sistema di tre equazioni di primo grado in tre incognite. Su ogni riga del sistema andremo a sostituire le coordinate del singolo punto nell’equazione della circonferenza.

In questa lezione vedremo come impostare e risolvere i problemi sul calcolo della circonferenza passante per tre punti, analizzando sia il metodo grafico (meno utilizzato perché meno preciso) e quello generalmente usato in geometria analitica.

I metodi usati

Quando ti viene assegnato a scuola o a casa un esercizio dal titolo: Calcolare la circonferenza passante per tre punti e ti vengono date le coordinate di questi ultimi, allora puoi decidere di scegliere due diversi metodi:

• Il metodo grafico o geometrico
• Il metodo algebrico o analitico

Metodo analitico

Il metodo algebrico è molto più facile dal punto di vista concettuale, non servono molti ragionamenti se non quello di imporre la condizione di appartenenza del punto alla figura. Per cui si sostituiscono, in tre diverse equqzioni le coordinate di ciascuno dei punti al posto della x e della y nell’equazione generale della circonferenza.

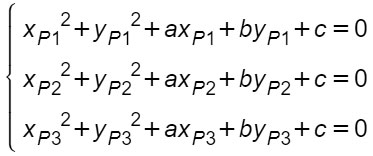
Si ottiene così un sistema di tre equazioni in tre incognite (a,b e c) che si può risolvere con il metodo di sostituzione oppure con somma/differenza.

Come puoi vedere dal punto di vista concettuale il metodo è molto sbrigativo, ma attenzione a non fare errori nello svolgimento del sistema. Basta un solo errore di segno e non si riuscirà mai a trovare una soluzione all’esercizio.

Metodo grafico e geometrico

E’ meno usato rispetto al primo metodo perché necessità di molti più passaggi, di ragionamento e della conoscenza di un teorema:

Considerato un triangolo inscritto in una circonferenza, il punto di intersezione degli assi dei lati del triangolo è il centro della circonferenza.

Approfondimento: Circocentro di un triangolo – il punto di intersezione degli assi

Si ricorda che l’asse di un segmento è perpendicolare a questo e passa per il suo punto medio. Possiamo quindi suddividere questo esercizio in vari step:

1. Si mettono i tre punti dati dalla traccia sul grafico, cioè sugli assi cartesiani.
2. Si uniscono i tre punti per disegnare il triangolo inscritto alla circonferenza da calcolare.
3. Si calcolano le rette corrispondenti ai tre lati – quindi si usa la formula della retta passante per 2 punti. In realtà bastano due rette per il calcolo.
4. Per i due lati calcolo il punto medio.
5. Di questi due lati, individuo la retta passante per il punto medio e di coefficiente angolare noto (si usa la m perpendicolare al lato).
6. Si intersecano le due rette appena determinate ed abbiamo trovato il centro della circonferenza per 3 punti.
7. Si fa la distanza dal centro con uno qualsiasi dei tre punti ed abbiamo il raggio.
8. Noti il raggio e il centro si può calcolare l’equazione della circonferenza per 3 punti.

Come hai potuto vedere si tratta di un metodo un po’ laborioso, cioè servono 9 passaggi per risolverlo ma i calcoli sono molto semplici da risolvere rispetto al metodo algebrico che vedremo dopo. Per renderti tutto più semplice, ti abbiamo proposto in basso alcuni esercizi svolti sul calcolo della circonferenza per tre punti.

Esercizi svolti ed esempi

Ti proponiamo ora un primo esempio in cui mettere in pratica i metodi che abbiamo appena visto. Risolveremo questo esercizio, cioè, sia con il metodo grafico e che con quello algebrico. Vediamo subito la traccia:

Determinare l’equazione della circonferenza passante per tre punti P1(2, 2), P2(3, 3), P3(6, 0) .

Svolgimento con il metodo analitico

Con questo metodo si fanno più calcoli, ma certamente riusciamo a calcolare l’equazione della circonferenza per tre punti in maniera più facile, ma attenzione a non fare errori di calcolo.

Iniziamo imponendo l’appartenenza di P1, P2 e P3 alla circonferenza, scrivendo 3 diverse equazioni da mettere a sistema.

*Il sistema è stato risolto con il metodo della somma e della differenza. Per far in modo che i coefficienti di a e b potessero essere sottratti tra loro abbiamo moltiplicato la prima riga per 3 e la seconda riga per 2. In questo modo si ottengono 6a e 6b in entrambe le equazioni che possono a questo punto essere sottratte.

Ti sarai accorto che i risultati sono differenti, ma se provi ad eseguire una scomposizione di polinomi, noterai che il risultato è identico.

Svolgimento con il metodo geometrico

La prima cosa da fare è disegnare sul grafico i tre punti ed unirli formando un triangolo.

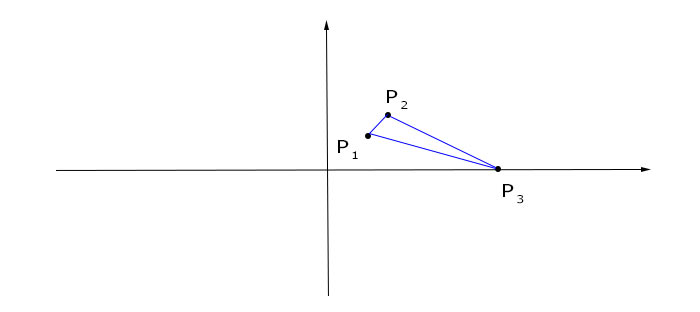
Invece di ragionare su tutti e tre i lati, mi occupo solo di due di loro. Basterà infatti mettere a sistema le equazioni dei loro due assi per ottenere il centro della circonferenza passante per i 3 punti dati. Dato che l’asse di un segmento è la retta che passa per il punto medio, inizio calcolando i punti medi dei lati P1-P2 e P1-P3. Avresti potuto scegliere anche il lato P2-P3, non sarebbe cambiato nulla.

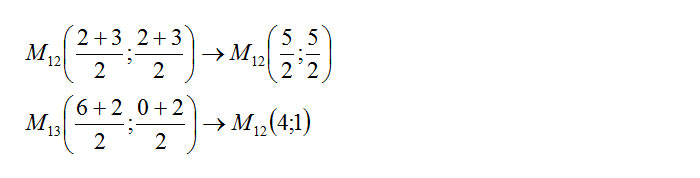
L’asse del segmento, inoltre, è perpendicolare ai lati. Ricordando la definizione di rette parallele e perpendicolari, per calcolare gli assi dei due lati che sto considerando ho bisogno delle equazioni delle loro rette. A quel punto mi basterà considerare il coefficiente angolare, cambiarlo di segno e “capovolgerlo”, cioè elevarlo a -1, per ottenere la m dell’asse del lato.

Uso allo scopo la formula della retta per 2 punti:

A questo punto mi basta utilizzare la formula della retta passante per 1 punto e coefficiente angolare noto. Avrò ottenuto così gli assi dei segmenti, cioè gli assi dei lati del triangolo inscritto alla circonferenza passante per 3 punti.

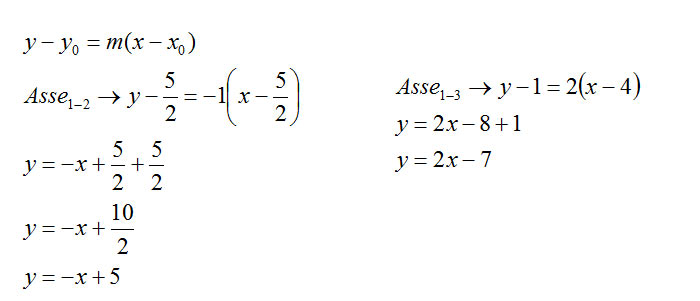
A questo punto mi basta sfruttare il teorema enunciato ad inizio lezione, cioè intersecare gli assi per ottenere il centro.

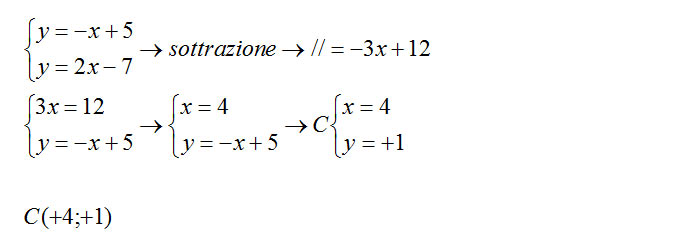
Per calcolare infine il raggio della circonferenza inscritta nel triangolo, cioè della circonferenza per 3 punti, mi basta calcolare la distanza dal centro da uno qualsiasi dei punti dati dalla traccia.

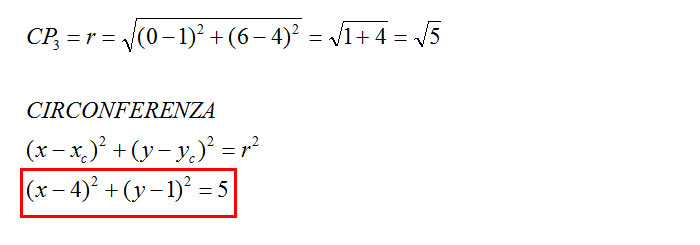
Tracce ed esercizi da risolvere

Puoi continuare ora ad esercitarti con le tracce che ti proponiamo di seguito. Ricordati che il nostro staff è a tua disposizione per chiarimenti e dubbi: contattaci e troverai risposta ad ogni domanda. Per ogni terna di punti che vedi di seguito, prova a calcolare l’equazione della circonferenza passante per 3 punti:

• A(0;2), B(2;4), C(1;0)
• A(0;0), B(6;0), C(0;3)
• A(1;2), B(0;-1), C(-1;+1)