In questa lezione vedremo come risolvere i problemi di geometria analitica in cui ci vengono assegnati dalla traccia il raggio della circonferenza e due punti appartenenti alla curva.
Questo tipo di esercizio somiglia moltissimo alla circonferenza per tre punti che abbiamo già studiato nelle precedenti lezioni. La differenza è che questa volta ci viene fornito il raggio. Ovviamente prima di affrontare questo tipo di esercizio, è bene che tu conosca quali sono le formule generali della circonferenza. Nel caso hai dubbi o perplessità ti consigliamo un rapido ripasso cliccando sul seguente pulsante.
Come si risolve?
Anche in questo caso sono necessarie tre equazioni per trovare le tre incognite del problema, a, b e c dell’equazione generale della circonferenza. Due ci vengono dalle condizioni di appartenenza dei due punti e l’ultima dalla dimensione del raggio. Si ottengono in questo modo tre equazioni che vanno messe a sistema. Risolvendolo si otterranno i tre coefficienti che andranno a formare l’equazione della circonferenza.
Un esempio concreto
Determinare l’equazione della circonferenza passante per due punti A(2;4) e B(0;2) e raggio pari a √10.
Innanzitutto c’è da precisare che non è detto che ci sia un’unica soluzione, cioè non possiamo ancora essere sicuri che ci sia una sola circonferenza passante per i due punti e con quel raggio. Per risolvere l’esercizio imponiamo la condizione di appartenenza dei 2 punti, cioè andiamo a sostituire le loro coordinate nell’equazione generale della circonferenza.
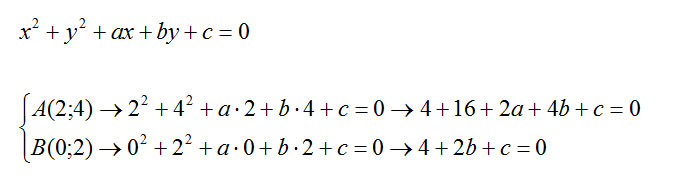
A queste due condizioni iniziali andiamo ad aggiungere il raggio usando la sua formula.
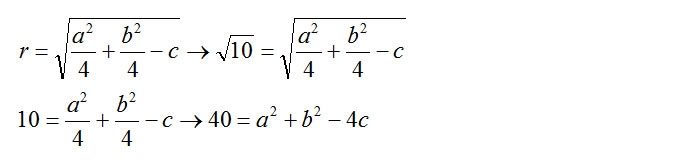
Posso così inserire le tre equazioni appena individuate in un unico sistema con tre incognite: a,b, c.
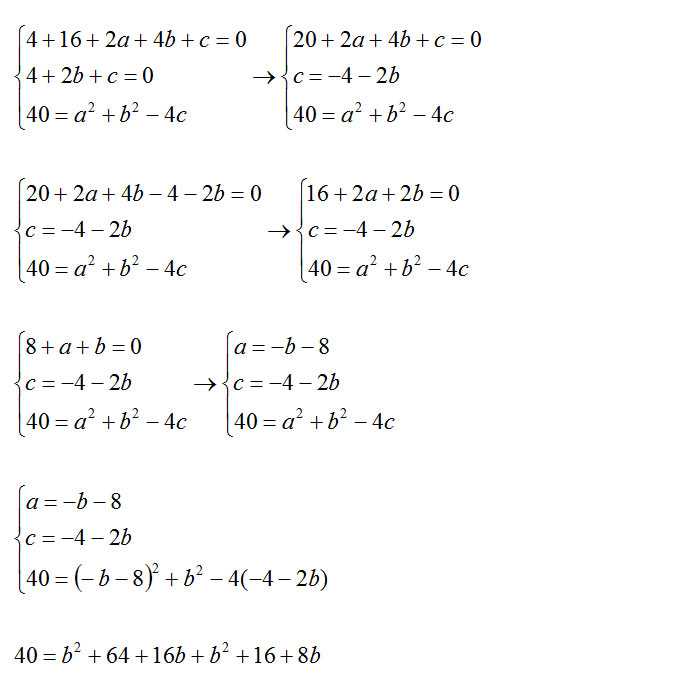
Il sistema è stato risolto con il metodo della sostituzione
Dall’ultima riga del sistema posso risolvere a questo punto come se fosse una normale equazione di secondo grado. Andando a scriverne le due soluzioni ottengo due valori di b. Questo significa che, con i dati che ci vengono forniti dall’esercizio, possiamo trovare due circonferenze per due punti e di raggio noto.
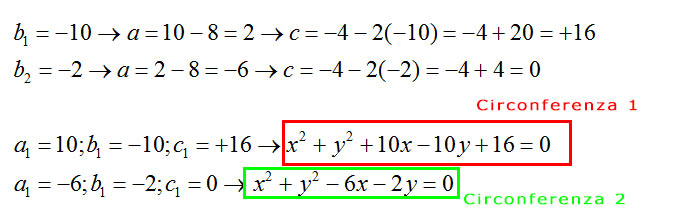
Considerazioni finali: Calcolare l’equazione della circonferenza per due punti e di raggio noto non è particolarmente difficile. E’ necessario tuttavia prestare molta attenzione a come svolgere il sistema di equazioni a 3 incognite. E’ bene fare tutti i calcoli e tutti i passaggi con molta attenzione, perché basta anche un solo segno sbagliato e il sistema porta a soluzioni errate o addirittura impossibili. Se si fanno tutti i passaggi l’esercizio, per quanto lungo, sarà molto facile da risolvere.
Tracce ed esercizi da risolvere
- Calcolare l’equazione della circonferenza passante per i punti A(2, 4), B(6, 8) e di raggio √10
- Calcolare l’equazione della circonferenza passante per i punti P1(0, 2), P2(4, 4) e di raggio √10
- Calcolare l’equazione della circonferenza passante per i punti A(0;0) e B(2;2) e di raggio √10
Come sempre lo staff di esercizi matematica è a tua disposizione in caso di perplessità o dubbi. Contattaci per ricevere assistenza con i tuoi esercizi o per ricevere chiarimenti sulla lezione che hai studiato.