In questa lezione troverai una facile e completa spiegazione sugli angoli associati, la tabella con le formule trigonometriche più importanti e alcuni esercizi svolti.
Definizione di archi associati
Quali sono?
Esempi ed esercizi svolti
Abbiamo visto nelle lezioni come calcolare seno e coseno e anche cotangente e tangente di un angolo e che è possibile risolvere esercizi di trigonometria con l’aiuto delle tabelle.
Queste però sono utili se gli angoli variano da 0 a 90°. Come risolviamo un’espressione trigonometrica se ho angoli maggiori di 90°?
Si utilizzano allora gli angoli associati o archi associati.
Archi o angoli associati
Per definizione gli angoli associati sono gli angoli:
![]()
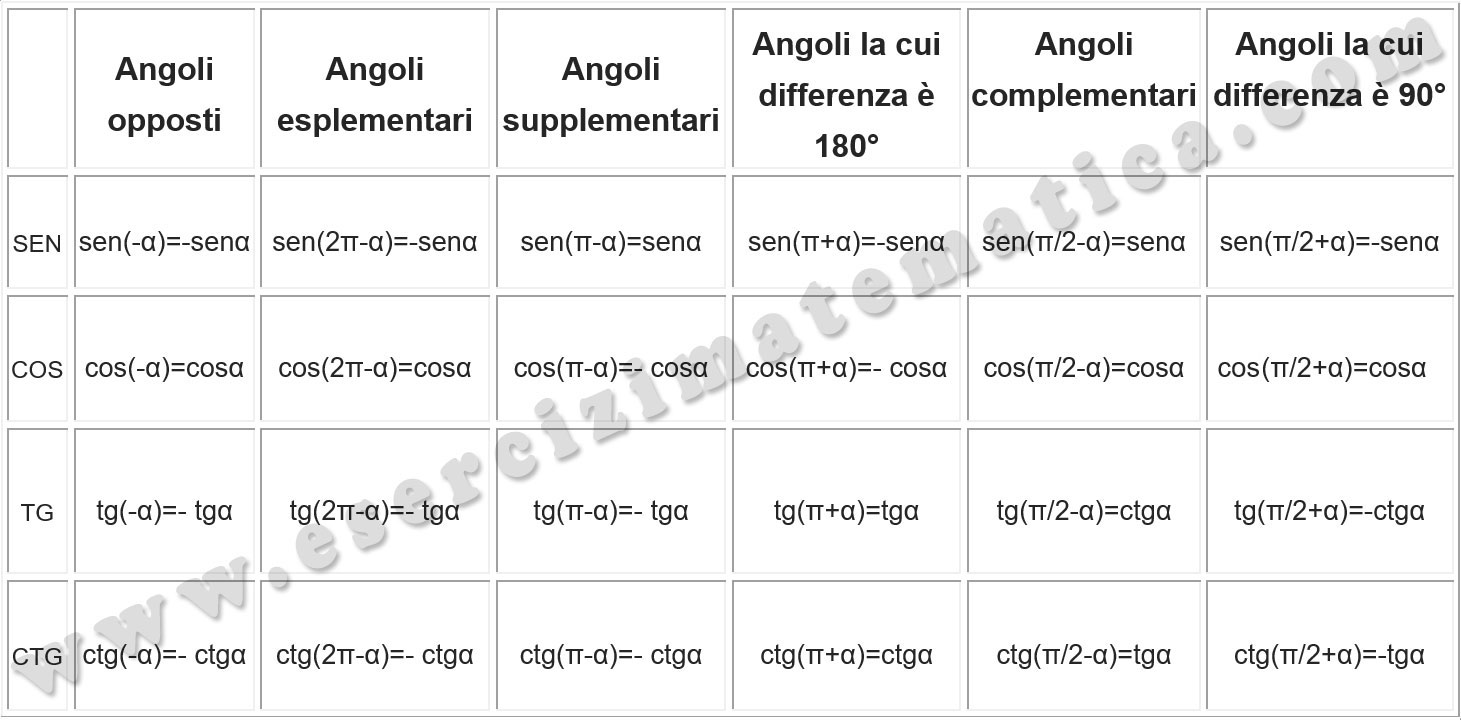
Cioè oltre all’angolo alfa, ci stiamo chiedendo come calcolare le funzioni trigonometriche per 180°-alfa, 180°+alfa e 360°+alfa. Ecco la tabella sugli archi associati che ti consigliamo di stampare e di memorizzare:
Lo schema sui valori degli archi associati ti permette di risolvere gli esercizi con angoli maggiori di 90°.
Tuttavia se vuoi una spiegazione degli archi associati più chiara e capire cosa significano queste formule possiamo far riferimento alla circonferenza goniometrica e trovare le relazioni che esistono tra i vari angoli.
Fate attenzione perché studiare gli archi associati attraverso il grafico vi aiuta a non dover ricordare a memoria le formule della tabella 🙂
Dimostrazione degli archi associati
Valori per 90-alfa – I quadrante
Nel primo quadrante possiamo trovare le relazioni tra l’angolo a e 90°-a: notate che il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al cos(90°-α), mentre il cosα, cioè il segmento OA, corrisponde al sen(90°-α) ossia il segmento OD (perché i triangoli rettangoli OAB e OCD sono uguali per il secondo criterio generalizzato di congruenza).
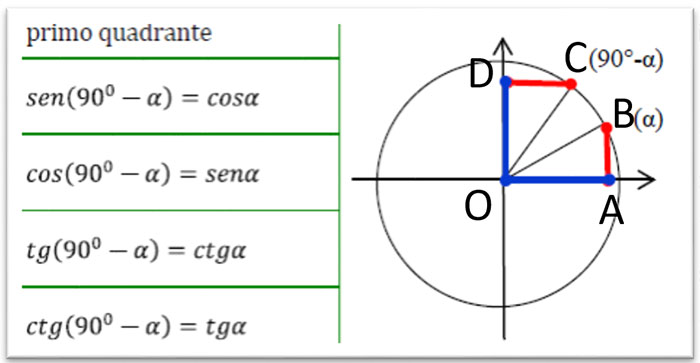
Angoli associati 90-a
Possiamo quindi concludere che il seno e il coseno si scambiano e sono entrambi positivi. Per ottenere la relazione di tangente e cotangente basta ricordare che la tangente è il rapporto tra seno e coseno, mentre la cotangente è il rapporto tra coseno e seno.
Valori di 90+alfa – II quadrante
Nel secondo quadrante troviamo le relazioni tra l’angolo a e 90°+a: in questo caso il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al cos(90°+α), mentre il cosα, cioè il segmento OA, corrisponde al sen(90°+α) ossia il segmento OD (perché i triangoli rettangoli OAB e OCD sono uguali per il secondo criterio generalizzato di congruenza).
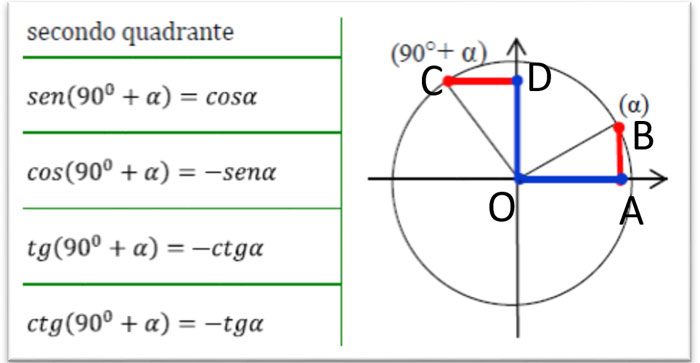
Tabella angoli associati 90+a
Quindi anche in questo caso si scambiano ma il coseno di 90° + a è negativo, infatti si trova sul lato sinistro dell’asse delle x.
Valori di 180-alfa: II quadrante
Nel secondo quadrante abbiamo anche le relazioni tra l’angolo a e 180°-a: in questo caso il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al sen(180°- α), mentre il cosα, cioè il segmento OA, corrisponde al cos(180°- α) ossia il segmento OC (perché i triangoli rettangoli OAB e OCD sono uguali per il secondo criterio generalizzato di congruenza).
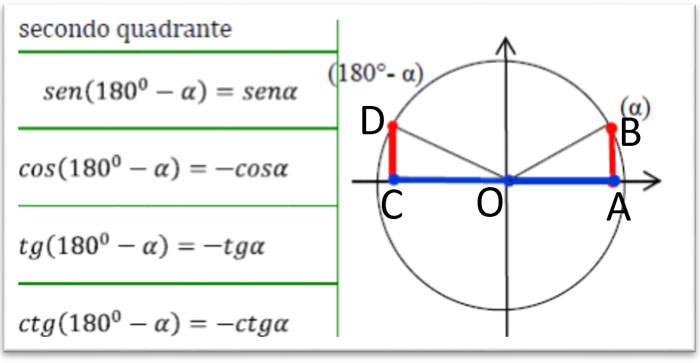
Tabella angoli associati 180-a
Notate che il disegno è specchiato rispetto all’asse delle y e quindi seno e coseno non si scambiano ma il coseno diventa negativo perché sul lato sinistro dell’asse delle x.
Valori di 180+alfa – III quadrante
Nel terzo quadrante abbiamo le relazioni tra l’angolo a e 180°+a: il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al sen(180°+ α), mentre il cosα, cioè il segmento OA, corrisponde al cos(180°+ α) ossia il segmento OD (perché i triangoli rettangoli OAB e OCD sono uguali per il secondo criterio generalizzato di congruenza).
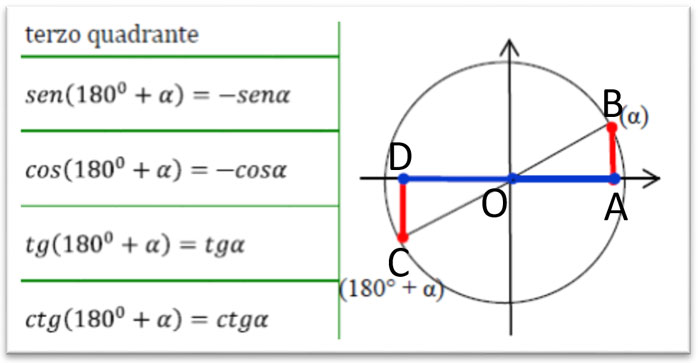
Tabella angoli associati 180+a
In questo caso seno e coseno non si scambiano ma diventano entrambi negativi.
Valori di 270-alfa: III quadrante
Sempre nel terzo quadrante abbiamo le relazioni tra l’angolo a e 270°-a: il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al cos(270°-α), mentre il cosα, cioè il segmento OA, corrisponde al sen(270°-α) ossia il segmento OD (perché i triangoli rettangoli OAB e OCD sono uguali per il secondo criterio generalizzato di congruenza).
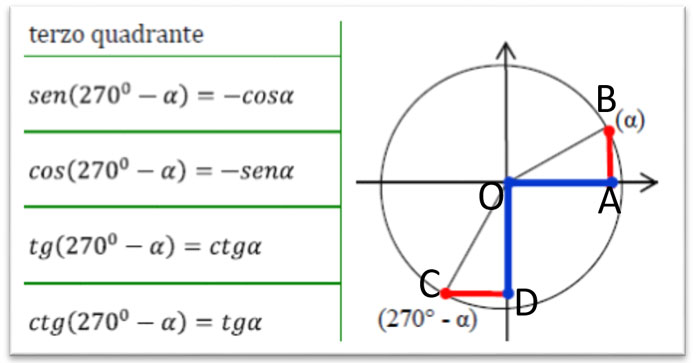
Tabella angoli associati 270-a
Il seno e il coseno si scambiano e sono entrambi negativi.
Valori di 270+alfa – IV quadrante
Nel quarto quadrante abbiamo le relazioni tra l’angolo a e 270°+a: il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al cos(270°+α), mentre il cosα, cioè il segmento OA, corrisponde al sen(270°+α) ossia il segmento OD (perché i triangoli rettangoli OAB e OCD sono uguali per il secondo criterio generalizzato di congruenza).
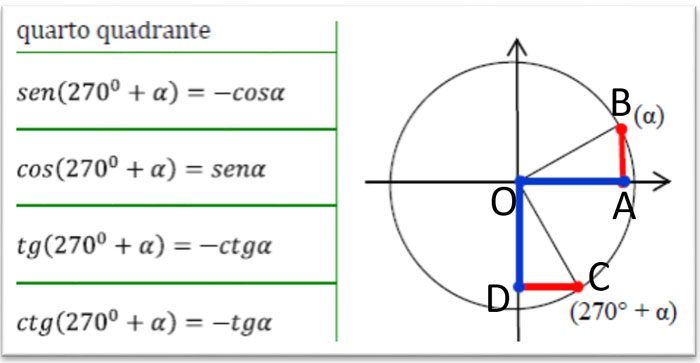
Tabella angoli associati 270+a
Il seno e il coseno si scambiano ed il seno diventa negativo.
Valori di 360-alfa – IV quadrante
Sempre nel quarto quadrante abbiamo le relazioni tra l’angolo a e 360°-a: il senα, cioè il segmento AB, è uguale al segmento AC che corrisponde al sen(360°- α), mentre il cosα, cioè il segmento OA, corrisponde al cos(360°- α) che è ancora il segmento OA (perché i triangoli rettangoli OAB e OAC sono uguali per il secondo criterio generalizzato di congruenza).
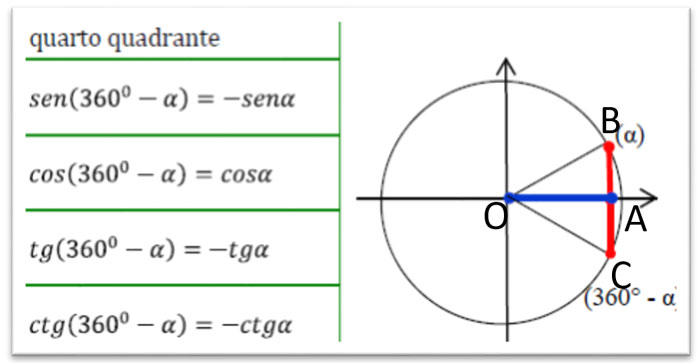
Tabella angoli associati 360-a
Il seno e il coseno non si scambiano ma il seno è negativo.
Valori di -alfa – IV quadranti
Ed infine nel quarto quadrante abbiamo anche le relazioni tra l’angolo a e -a: come si può vedere il disegno è identico al caso di 360°-a e quindi si hanno le stesse relazioni.
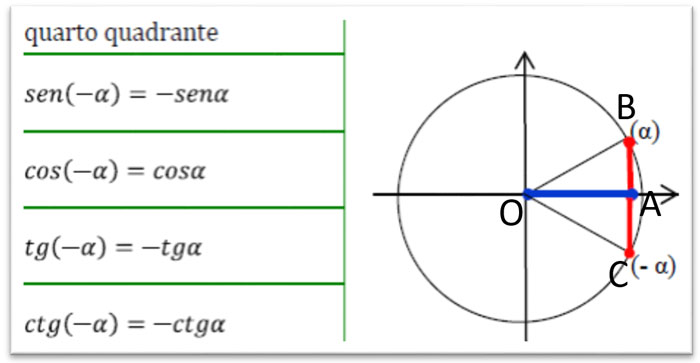
Angoli associati negativi
Esercizi svolti sugli archi associati
3cos(120°)=
Per svolgere questa espressione trigonometrica ricordiamo la regola degli archi associati e cerchiamo la relazione che il nostro angolo, in questo caso 120°, può avere con pigreco/2, p, 3/2pigreco, 2pigreco.
Notiamo che possiamo scrivere il nostro angolo 120° in due diversi modi:
120°=180°-60° cioè 180°-a
120°=90°+30° cioè 120°-a
Nel primo caso a=60°, mentre nel secondo a=30°. Svolgiamo l’esercizio scegliendo l’uguaglianza 120°=180°-a con a = 60° (ovviamente il risultato sarebbe lo stesso se scegliessimo a = 30°), quindi
3 cos (120°) = 3 cos (180°- 60°) =
Cerchiamo sulla tabella degli archi associati a cosa corrisponde il cos(180°-a).
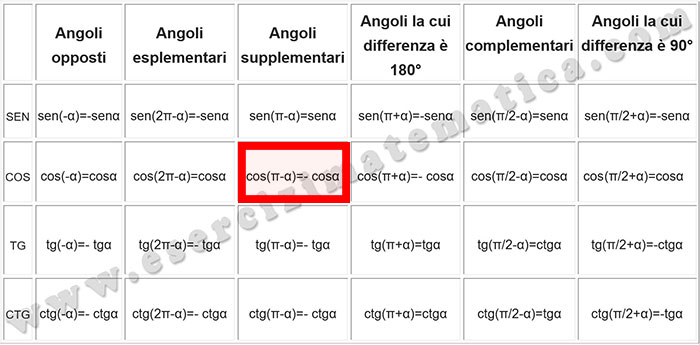
Troviamo così la relazione cos(180°-a)=-cosa e quindi
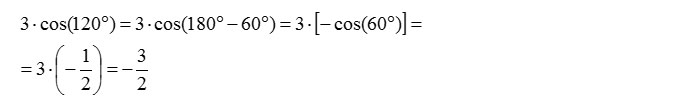
Dal punto di vista grafico vediamo che siamo nel caso in cui il disegno è specchiato rispetto all’asse delle y: senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al sen(180°-α), mentre il cosα, cioè il segmento OA, corrisponde al cos(180°- α) ossia il segmento OC che è negativo perché sia trova sul lato sinistro dell’asse delle x.

cotg(270°)=?
Anche per questa espressione trigonometrica utilizziamo le regole degli archi associati. Notiamo che possiamo scrivere il nostro angolo 270° in due modi differenti:
270°=180°+90° cioè 180°+a
270°=360°-a cioè 360°-a
Scegliamo la prima uguaglianza e cerchiamo sulla tabella a cosa corrisponde la ctg(180° +a). Anche in questo caso la scelta dell’arco associato è assolutamente arbitraria: avremmo potuto anche scegliere 360-a il risultato sarebbe rimasto invariato.
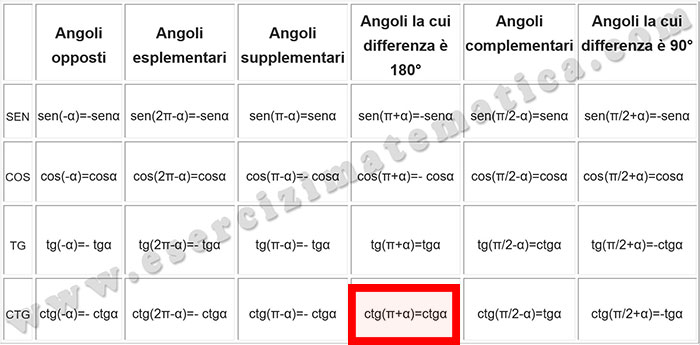
Troviamo così la relazione ctg (180°+a )=ctga e quindi
![]()
Dal punto di vista grafico siamo nel terzo quadrante e il senα, cioè il segmento AB, è uguale al segmento DC che corrisponde al sen(180°+ α), mentre il cosα, cioè il segmento OA, corrisponde al cos(180°+ α) ossia il segmento OD.
Per esercitarti verifica che il risultato sia lo stesso scegliendo la seconda formula degli archi associati proposta dall’esercizio, cioè 270° = 360° – a e quindi a = 90°.
A questo link trovi altri esercizi sugli archi associati. Se hai bisogno di una mano a risolvere questi problemi o quelli che hai assegnati a scuola, puoi contattarci, restiamo sempre a tua disposizione.
davvero buon aiuto, grazie!